50. Дайте определение узкополосного сигнала.
51. Для узкополосного сигнала определите понятие комплексной огибающей.
6.1. Введение. Краткие сведения по теории функций комплексной переменной
Решение многих задач радиотехники, связанных, например, со спектральным анализом сигналов, изучением распространения электромагнитных волн в различных средах, исследованием пространственно-временной структуры электромагнитного поля в резонаторах, волноводах и излучающих системах, синтезом фильтров, этот список можно продолжить, приводит к использованию различных специальных функций. Иногда вместо термина специальные функции используют термин высшие трансцендентные функции, оставляя название элементарные функции за степенными, показательными, логарифмическими и тригонометрическими. Обычно в класс специальных включают гамма- и бета-функции, интегральную показательную функцию и родственные ей, интеграл ошибок и связанные с ним функции, дзета-функцию Римана, эллиптические интегралы, классические ортогональные полиномы и функции Бесселя. Для знакомства со специальными функциями нам потребуется освежить в памяти читателя основные понятия теории функций комплексного переменного. Более подробную информацию можно получить в многочисленных руководствах по данному разделу математики [12].
Говорят, что на множестве
M точек плоскости ![]() задана функция
задана функция ![]() , если известно правило, по которому каждой
точке z из M ставится в соответствие определённая точка или
совокупность точек
, если известно правило, по которому каждой
точке z из M ставится в соответствие определённая точка или
совокупность точек ![]() . В первом случае функция f(z)
называется однозначной, а во втором – многозначной.
. В первом случае функция f(z)
называется однозначной, а во втором – многозначной.
Обычно под множеством M понимают область D, для которой выполняются следующие условия:
– для каждой точки из D этому множеству принадлежит и достаточно малый круг с центром в этой точке (свойство открытости);
– любые две точки D можно соединить ломанной, все точки которой принадлежат D (свойство связанности).
Граничной точкой области
называют такую точку, которая сама не принадлежит D, но в любом сколь
угодно малом круге с центром в этой точке содержатся точки из D.
Совокупность граничных точек называют границей области. Область D, с
присоединённой к ней границей, называют замкнутой и обозначают ![]() .
.
Как и для операторов и обычных функций множество M называется множеством, а в случае области – областью определения, а совокупность всех значений, которые f(z) принимает на M – множеством (областью) значений.
Как видно из введённых
обозначений ![]() и
и ![]() ,
задание функций комплексного переменного равносильно заданию двух функций двух
действительных переменных x и y, а именно
,
задание функций комплексного переменного равносильно заданию двух функций двух
действительных переменных x и y, а именно ![]() и
и
![]() . Например,
. Например,
![]() ,
,
и по условию равенства комплексных
чисел ![]() , а
, а ![]() . Для
функции
. Для
функции ![]() и
и ![]() , а
, а ![]() .
.
Важнейшими понятиями для функций комплексного переменного являются понятия предела, непрерывности и аналитической функции.
Функция f(z)
имеет предел в точке ![]() , если она однозначна и
определена в окрестности этой точки и существуют пределы
, если она однозначна и
определена в окрестности этой точки и существуют пределы
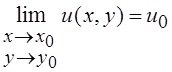 и
и 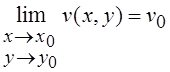 ,
,
что обозначают как 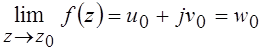 .
.
Другое определение звучит так:
условие 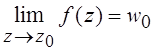 выполняется тогда и только тогда, когда
для
выполняется тогда и только тогда, когда
для ![]() , так что из неравенства
, так что из неравенства ![]() вытекает
вытекает ![]() .
.
Важно подчеркнуть, что
если предел существует, то z может стремиться к z0 по любому пути. Функция f(z) называется
непрерывной в точке z0,
если она определена в окрестности этой точки, включая саму эту точку z0, и 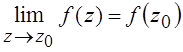 . Необходимыми и
достаточными условиями непрерывности f(z) в точке z0 является непрерывность функций u(x, y)
и v(x, y) в точке (x0, y0).
Функция называется непрерывной в области D, если она непрерывна в каждой
точке этой области.
. Необходимыми и
достаточными условиями непрерывности f(z) в точке z0 является непрерывность функций u(x, y)
и v(x, y) в точке (x0, y0).
Функция называется непрерывной в области D, если она непрерывна в каждой
точке этой области.
Для функции f(z)непрерывной в замкнутой области ![]() справедливы следующие
утверждения:
справедливы следующие
утверждения:
–
f(z) ограничена в ![]() , т. е. существует такая постоянная M,
что для всех z из
, т. е. существует такая постоянная M,
что для всех z из ![]() :
: ![]() ;
;
–
f(z) достигает в ![]() своего наибольшего и наименьшего значений,
т. е.
своего наибольшего и наименьшего значений,
т. е. ![]() , что для
, что для ![]() и
и ![]() ;
;
–
f(z) равномерно непрерывна, т.
е. для ![]() , зависящее только от ε, так что для
любой пары точек z1 и z2 из
, зависящее только от ε, так что для
любой пары точек z1 и z2 из ![]() из неравенства
из неравенства ![]() следует неравенство
следует неравенство ![]() .
.
Условия
дифференцируемости функции ![]() дают так называемые
условия Даламбера–Эйлера или Коши–Римана: функция f(z), определённая
в некоторой окрестности точки z и имеющая в этой окрестности
дифференцируемые вещественную u(x, y) и мнимую v(x,
y) части, является дифференцируемой, если u(x, y) и v(x,
y) удовлетворяют условиям:
дают так называемые
условия Даламбера–Эйлера или Коши–Римана: функция f(z), определённая
в некоторой окрестности точки z и имеющая в этой окрестности
дифференцируемые вещественную u(x, y) и мнимую v(x,
y) части, является дифференцируемой, если u(x, y) и v(x,
y) удовлетворяют условиям:
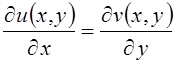 ,
, 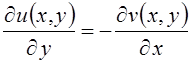 . (6.1)
. (6.1)
Функция f(z), дифференцируемая в каждой точке
некоторой области, называется аналитической в данной области. Например, функция
![]() аналитична на всей плоскости комплексного
переменного z. Её однозначность очевидна. Проверим выполнение условия (6.1).
аналитична на всей плоскости комплексного
переменного z. Её однозначность очевидна. Проверим выполнение условия (6.1).
![]() , т. е.
, т. е.
![]() ,
, ![]() .
.
Тогда
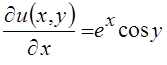 ;
; 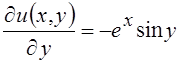 ;
;
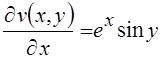 ;
; 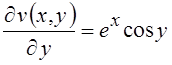 .
(6.2)
.
(6.2)
Из (6.2) видно, что условия Даламбера–Эйлера выполняются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.