Линейные операторы и функционалы. Часть 2

необходимо и достаточно, чтобы он был самосопряженным оператором и для каждого  выполнялось равенство .

Радиотехническим примером проектора может служить оператор полосовой фильтрации с прямоугольной единичной АЧХ и нулевой ФЧХ. Такой оператор отображает множество входных сигналов на множество сигналов с финитным спектром. Во временной области проектором будет линейный ключ, для которого .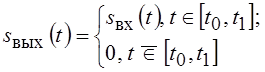

Рассмотрим линейные операторы, наиболее часто встречающиеся в задачах радиотехники.

Оператор Фурье.

Оператор Фурье F определяется на множестве функций L₂ или L₁ и с метрико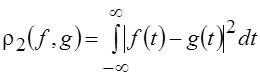й  или 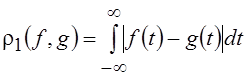 соответственно. Прямое преобразование Фурье (оператор Фурье) определяется как

,

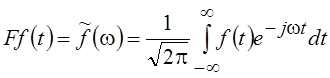а обратное (обратный оператор) как

.

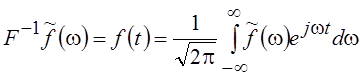В радиотехнике преобразование Фурье сигнала s(t) называют спектральной плотностью  или просто спектром, причем прямое преобразование записывается как

,

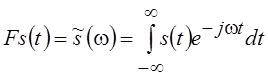а обратное как

.

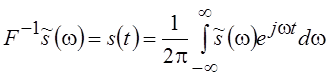Модуль функции  называют амплитудно-частотным, а аргумент
 – фазочастотным спектром. Амплитудный спектр, равный 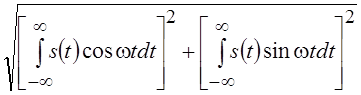 является четной функцией w, а фазовый 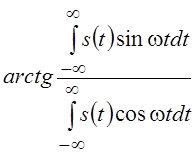 – нечетной.

Для четных сигналов s(t) = s(–t) интеграл 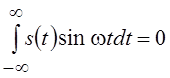 и амплитудный спектр определяется косинусным преобразованием Фурье и равен 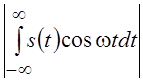. Для нечетных сигналов s(t) = –s(t) амплитудный спектр равен .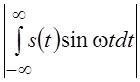

Приведем для иллюстрации спектры часто встречающихся сигналов, пользуясь «радиотехническим» способом определения оператора Фурье.

1. Прямоугольный видеоимпульс .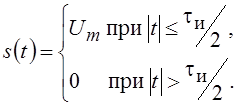

.

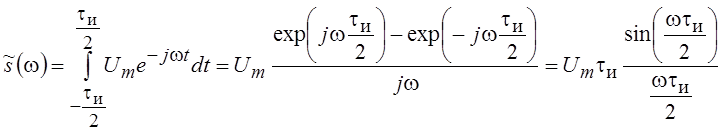2. Односторонний экспоненциальный сигнал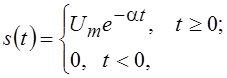  
a > 0 .

.

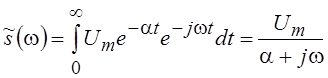3. Колокольный или гауссовский импульс , a > 0.

.

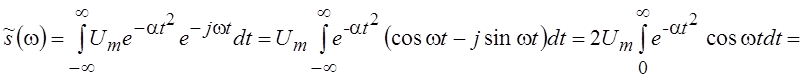
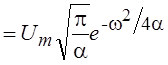Таким образом, спектр гауссовского импульса имеет тот же функциональный вид, что и сигнал. К этому интересному факту мы еще вернемся.

Для абсолютно интегрируемых функций f(t) Î L₁ преобразование Фурье  равномерно непрерывно[*] и ограничено при wÎ(–¥, ¥), причем  при |w| ® ¥.

Ядром оператора Фурье является функция двух переменных 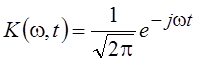, из симметрии которой по обеим переменным следует самосопряженность оператора Фурье. Оператор Фурье является унитарным, так как его ядро удовлетворяет условию (5.4), т. е. 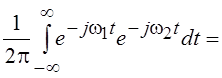 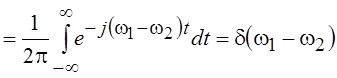. Эта запись означает, что преобразование Фурье функции f(t) = 1 при t Î(–¥, ¥) есть дельта-функция. Преобразование Фурье дельта-функции 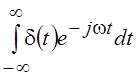 в соответствии с фильтрующим свойством дельта-функции есть функция j(w) = 1 при wÎ(–¥, ¥). На радиотехническом языке это означает, что спектр бесконечно короткого импульса равномерен. Это позволяет при анализе линейных цепей заменять входной импульс дельта-функцией, умноженной на площадь импульса, если длительность входного сигнала много меньше длительности импульсной характеристики h(t) или ширина спектра сигнала много больше полосы пропускания системы.

Напомним, что импульсной характеристикой называется отклик линейной цепи на воздействие в виде дельта-функции d(t).

Унитарность преобразования Фурье объясняет, почему обратное преобразование (обратный оператор) F ^–1 имеет вид

.

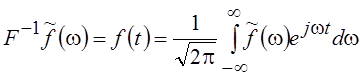Ведь для унитарного самосопряженного оператора ядро обратного оператора есть комплексное сопряжение исходного ядра.

Так как унитарный оператор не меняет скалярного произведения, то, следовательно, справедливо равенство 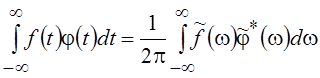, называемое обобщенным равенством Парсеваля. Если f(t) = j(t) = s(t), то

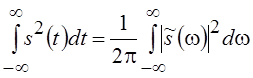                                       (5.5)

Интерпретируя s(t) как падение напряжения на резисторе сопротивлением в 1 W, можно считать s²(t) мгновенной мощностью, а интеграл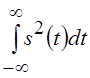 равен энергии сигнала Е. Таким образом, равенство (5.5) позволяет определить энергию сигнала как через его временное представление s(t), так и через спектр .

Обобщенное равенство Парсеваля и соотношение (5.5) часто называемое теоремой Рэлея, записаны при использовании преобразования Фурье в «радиотехнической» форме, т. е. .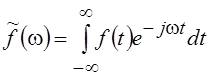

Собственные значения и собственные функции оператора Фурье удовлетворяют интегральному уравнению Фредгольма .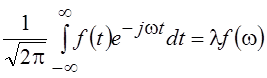

Одну собственную функцию мы уже знаем. В самом деле, если записать преобразование Фурье для функции , то в соответствии с примером 3, рассмотренным выше, получим . Таким образом,  является собственной функцией оператора Фурье ,отвечающей собственному значению 1. Можно показать, что множество собственных функций оператора Фурье, образующих в соответствии с теоремой Гильберта-Шмидта базис в L₂, имеет вид 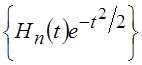, где H_n(t) – уже знакомые нам полиномы Эрмита. Функции  называют функциями Эрмита.

Рассмотрим основные свойства оператора Фурье, часто называемые теоремами о спектрах, пользуясь определением .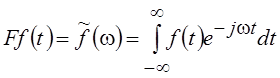

1.  Теорема смещения.

Пусть сигнал s(t) имеет спектр . Найдем спектр смещенного сигнала s(t – t), т. е. вычислим 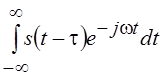. Делая замену переменной х = t – – t, получим, что спектр смещенного на время t сигнала равен произведению исходного спектра  на . Так как операция смещения сигнала во времени реализуется с помощью линии задержки, то  является комплексным коэффициентом передачи (частотной характеристикой) идеальной линии задержки.

Рассмотрим спектр сигнала , равный 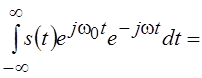 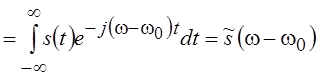. Как видно из полученного выражения, смещение спектра на величину w₀ в частотной области соответствует умножению сигнала на .

Если сигнал s(t) умножается на функцию cos w₀t (этот процесс называется модуляцией), то учитывая, что 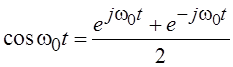, получим следующее выражение для спектра сигнала s(t) cos w₀t:

.

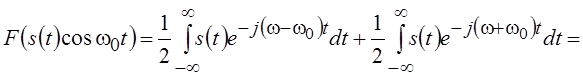
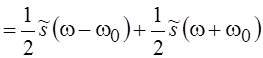Таким образом, спектр модулированного сигнала состоит из двух слагаемых, совпадающих по форме с исходным спектром , сдвинутых вправо и влево на величину w₀ и умноженных на коэффициент 0.5.

2.  Посмотрим, что произойдет со спектром сигнала s(t) при изменении масштаба времени, т. е. при переходе к сигналу s(kt), где k > 0 – масштабный коэффициент, определяющий при k >1 сжатие сигнала, а при k < 1 растяжение.

Преобразование Фурье для сигнала s(kt) будет иметь вид 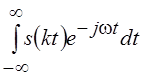 и после замены переменной х = kt получим, что искомый спектр равняется 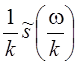. Если k < 0, то спектр преобразованного сигнала будет равен 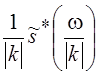 или 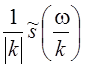. Это утверждение читателю предлагается проверить самостоятельно.

3.  Спектры производной и интеграла.

Пусть сигнал s(t) дифференцируем и обращается в ноль при t ® ±¥. Тогда, интегрируя по частям выражение для спектра производной  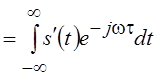, получим , т. е. операция дифференцирования подчеркивает высокие частоты в спектре исходного сигнала. При n-кратном дифференцировании .

Спектр интеграла от сигнала 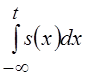 будет равен  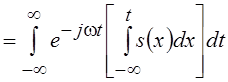. Интегрируя по частям и считая, что 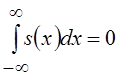, получим 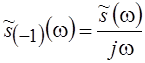. Заметим, что спектр определенного интеграла, как спектр константы, равен произведению этой константы на d(w).