Общая постановка задачи оптимизации металлургических процессов, страница 4

В металлургии: проектирование агрегатов (размеры, форма).

Метод сводит задачу с ограничениями к обычной экстремальной задаче без ограничений.

Метод множителей Лагранжа часто применяют в качестве вспомогательного средства в других методах оптимизации, таких как вариационное исчисление и динамическое программирование.

Постановка задачи

Найти такие оптимальные значения управляющих параметров х₁^*, х₂^*, …, х_n^*, дающие экстремум функции G(х₁, х₂, …, х_n) ® extr при ограничениях

h_j(х₁, х₂, …, х_n) = b_j,

где i = 1, …, n – переменные; j = 1, …, m – ограничения.

Метод решения

Составляется вспомогательная функция

.

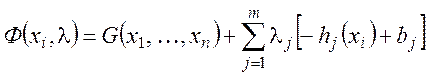Необходимое условие

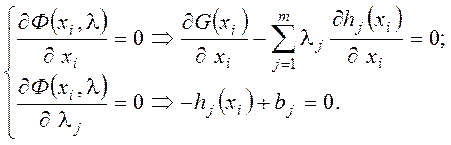
Находим х_n^*, которые будут удовлетворять и min, и max, и седловым точкам, и точкам перегиба.

Достаточные условия: определитель матрицы вторых производных

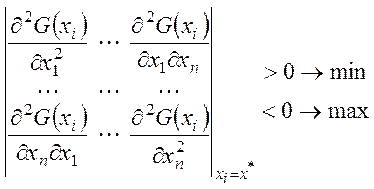
Если функция G имеет несколько экстремумов, то найденные решения проверяют по определителю и выбирают абсолютный min или max.

Пример 1. Найти минимум функции

G(х₁, х₂) = x₁² + x₂²

при ограничении                               x₁ + x₂ = 4.

Функция Лагранжа имеет вид

Ф(х₁, х₂, l) = x₁² + x₂² + l(4 – x₁ – x₂).

Соответствующие условия минимума можно записать следующим образом:

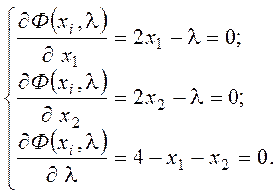
Решением этой системы уравнений является x₁ = x₂ = 2, l = 4. Матрица Гессе функции Ф имеет вид

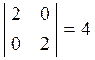
и, следовательно, положительно определена. Поэтому точка x₁ = x₂ = 2 является точкой минимума.

Теорема Куна-Таккера

Метод множителей Лагранжа можно использовать при построении критериев оптимальности для задач оптимизации с ограничениями в виде равенств.

Кун и Таккер обобщили этот подход на случай задачи нелинейного программирования с ограничениями как в виде равенств, так и в виде неравенств.

Постановка задачи

Найти такие оптимальные параметры х₁^*, х₂^*, …, х_n^*, дающие экстремум функции

G(х₁, х₂, …, х_n) ® extr

при ограничениях

	hj(хi) £ bj (j = 1, …, k),	(1)
	hj(хi) ³ bj (j = k + 1, …, m),	(2)
	хi ³ 0.	(3)

Требуется найти необходимые условия существования экстремума.

h_j(х_i) + х_ik = b_j (j = 1, …, k)

h_j(х_i) – х_im = b_j (j = k + 1, …, m),

х_i – х_u = 0 (i = 1, …, n).

		(4)
		(5)

Анализируя уравнения (5) можно получить систему уравнений

(6)

Система (6) – условия Куна-Таккера.

Для того чтобы экстремум функции G(хi) был достигнут в точке хi*при условиях (1), (2), (3) необходимо и достаточно требовать существования таких lj*, при которых х* и l* является седловой точкой функции Ф(х, l).

Пример 2. Найти х1 и х2, максимизирующие функцию G(х1, х2) = =– 8x12 – 10x22 + 12х1х2 – 50х1 + 80х2 при ограничениях x1 + x2 £ 1; 8x12 + x22 £ 2; x1 ³ 0; x2 ³ 0. Составим функцию Лагранжа Ф(xi, l) = – 8x12 – 10x22 + 12х1х2 – 50х1 + 80х2 + l1(1 – x1 – x2) + l2(2 – 8x12 – x22). Записываем условия Куна-Таккера. Первое ограничение есть прямая, второе есть внутренняя область эллипса .

Общая часть (пересечение) этих областей образует выпуклую область допустимых значений. Если построить семейство кривых уровня целевой функции G(х₁, х₂) = с, то касание с допустимой областью происходит в вершине с координатами (0,1) и это есть решение задачи.

Следовательно,

Таким образом, условия Куна-Таккера для рассматриваемой точки выполняются. Другие точки этим условиям не удовлетворяют.

Необходимые условия Куна-Таккера позволяют идентифицировать стационарные точки в нелинейной задаче с ограничениями в виде неравенств. Они являются также достаточными, если в задаче максимизации (минимизации) целевая функция вогнутая (выпуклая), а область допустимых решений является выпуклым множеством.

Теорема позволяет расширить круг задач нелинейного программирования, решение которых может быть получено в аналитическом виде.

Линейное программирование

Это совокупность методов решения экстремальных задач, в которых целевая функция и ограничения задачи заданы линейными уравнениями.