Общая постановка задачи оптимизации металлургических процессов, страница 3

Метод классического анализа

Математическая формулировка оптимальной задачи часто эквивалентна задаче отыскания экстремума функции одной или нескольких переменных. Поэтому для решения таких задач могут быть использованы различные методы исследования функции классического анализа.

Данные методы применяются для решения задач выбора аппаратурного оформления и определения оптимальных условий протекания некоторых металлургических процессов.

Применяется в случаях, когда известен аналитический вид оптимизируемой функции G(x). Это позволяет найти в аналитическом виде производные оптимизируемой функции G(x), используя которые и формируются необходимые и достаточные условия существования экстремума.

Виды экстремума функции одной переменной

а)		б)
в)	г)		д)

На рисунках б) и в) показаны функции, когда экстремум не существует.

Для рисунка г) производная равна нулю, но это не экстремум, требуется дополнительное исследование.

Необходимым условием существования экстремума G(x) при отсутствии ограничений на диапазон изменения переменной x могут быть получены из анализа первой производной .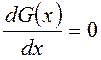

Достаточные условия существования экстремума:

-  сравнение значений функций;

-  сравнение знаков производных;

-  исследование знаков высших производных.

Если G(xk–e) и G(xk+e) одновременно больше или меньше G(xk), то в точке xk – экстремум. Если знак производной меняется при переходе через точку xk, то экстремум. Меняется с (+) на (–), то max; с (–) на (+), то min Если порядок первой необращающейся в нуль в точке xk производной четный, то в данной точке есть экстремум функции G(x), который будет max или min в зависимости от знака этой производной: < 0 – max; > 0 – min.

Алгоритм:

1)  Находятся все точки, подозреваемые на экстремум.

2)  Эти точки исследуются на экстремум. Строится график.

3)  Среди локальных экстремумов определяют глобальный.

Пример 1. Исследовать характер точек перегиба функции

f(x) = x³ – 2x² + x + 1.

Первая производная .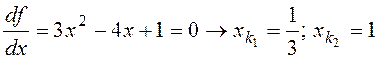

Вторая производная

.

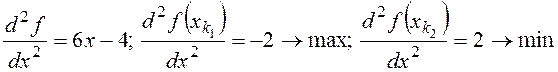Пример 2. Исследовать на экстремум f(x) = (x – 1)⁶.

Первая производная .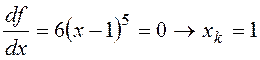

Вторая производная .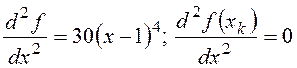

Первой необращающейся в нуль в точке x_k = 1 производной будет 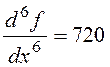, т.е. производная шестого (четного) порядка. Следовательно, функция f(x) имеет min в точке x_k = 1.

Экстремумы функции многих переменных

Решение задачи оптимизации существенно усложняется, когда критерий оптимизации является функцией нескольких независимых переменных, даже при известном аналитическом выражении этой функции G = G(x₁, x₂, …, x_n).

Наибольшие трудности возникают при отсутствии непрерывности некоторых производных оптимизируемой функции.

В этом случае целесообразно использовать методы нелинейного программирования (численные методы).

Необходимое условие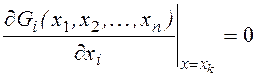

Достаточные условия (из исследования определителей)

D₁ = а₁₁ > 0; ; ; .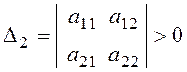

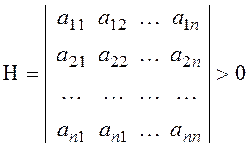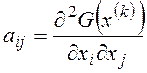Симметричная матрица n´n элементов вида а_ij называется гессианом (матрицей Гессе).

Если все главные миноры матрицы Гессе положительны, то в точке x_k min; если матрица отрицательно определена, т.е. происходит чередование знаков D₁ < 0; D₂ > 0; D₃ < 0, … и.т.д., то в точке x_k max.

Пример 3. Дана функция

f(x) = x₁ + 2x₃ + x₂x₃ – x₁² – x₂²– x₃².

Из необходимого условия

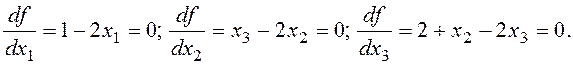
Решением этой системы является вектор 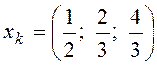. Чтобы проверить выполнение достаточного условия, вычислим матрицу Гессе:

.

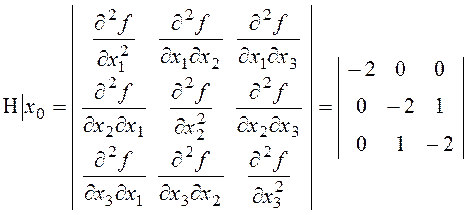Угловые главные миноры  равны –2, 4 и –6, соответственно. В этом случае  является отрицательно определенной матрицей, следовательно, 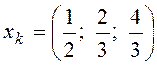 – точка максимума.

Метод множителей Лагранжа

Предназначен для отыскания экстремума критерия оптимальности при условии, что на независимые переменные наложены определенные ограничения, имеющие вид равенств.

Типичными примерами подобных задач служат задачи, в которых требуется оптимальным образом распределить заданное количество ресурсов, чтобы принятая оценка эффективности процесса имела при этом max или min значение.