Теорема:
Если одна СЛУ получается из другой СЛУ путем эквивалентных преобразований со строками расширенной матрицы исходной системы, то эти СЛУ равносильны.
Эта теорема дает самый естественный метод решения СЛУ, который носит название метода Гаусса:
1) расширенную матрицу системы эквивалентными преобразованиями со строками приводят к ступенчатому виду;
2) записывают систему, которая соответствует полученной ступенчатой матрице (система равносильна исходной);
3) пишут ответ (для СЛУ с матрицей ступенчатого вида это очень легко сделать).
Пример 1.
Решить СЛУ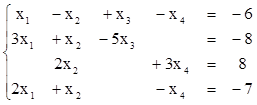 
Решение:
Запишем расширенную матрицу системы и приведем ее эквивалентными преобразованиями к ступенчатому виду.
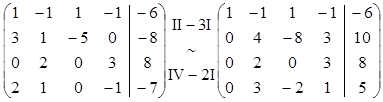
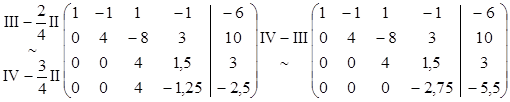
Новая СЛУ, равносильная исходной:
23
Задаем произвольно две любые координаты точки, третью находим из уравнения.
] х=0, у=0 Þ 3×0+2×0-z=5 Þ z=5
(×)М1(0,0,-5) принадлежит геометрическому образу уравнения
] х=4, z=7 Þ 3×4+2y-7=5 Þ y=0
(×)М2(4,0,7) принадлежит геометрическому образу уравнения
] y=-8, z=6 Þ 3x-2×8-6=5 Þ x=9
(×)М3(9,-8,6) принадлежит геометрическому образу уравнения
и т.д.
Как правило, геометрическим образом одного уравнения в пространстве F(x,y,z)=0 является поверхность.
Для того,
чтобы задать линию в пространстве, необходима система уравнений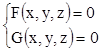 
.
Каждое из уравнений системы задает поверхность, а нужная линия – это линия пересечения этих поверхностей.
Например, геометрическим
образом уравнения z=5 является множество всех точек М(х,у,5), где х, у – любые
числа, т.е. плоскость, ôô плоскости ХОY и проходящая через
точку (0,0,5) на оси OZ.
Геометрическим образом системы уравнений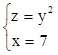 
будет
линия, парабола в плоскости, проходящей через точку (7,0,0) и параллельной
плоскости YOZ.
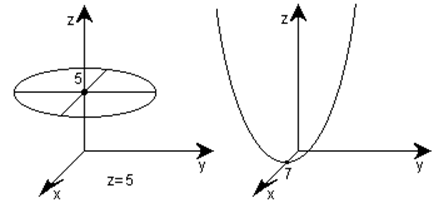
Заметим, что если в уравнении линии или
поверхности отсутствует одна из координат, то линия или поверхность параллельна
соответствующей оси. Например, поверхность 
параллельна
оси ОХ.
40
который при подстановке в СЛУ обращает любое уравнение в верное равенство.
Пример.
Решением системы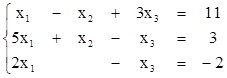 
является х1=1, х2=2, х3=4. Убедимся в этом, подставив предложенные значения х1, х2, х3 в СЛУ.
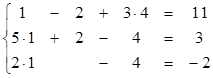
Все уравнения СЛУ обратились в верные равенства, данный набор чисел – действительно является решением СЛУ.
СЛУ вида (1) часто записывают в матричной форме, вводя обозначения:
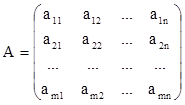- матрица
коэффициентов СЛУ,
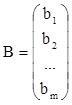- вектор-столбец
правых частей,
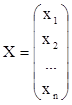- вектор – столбец
неизвестных.
Тогда СЛУ (1) можно записать:
(2)
Наиболее распространенная условная запись (1):
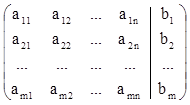. (3)
21
Решение:
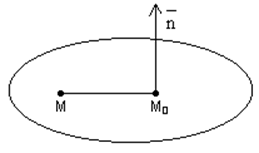
Если точка МÎплоскости a,
то 
^
и наоборот.
=(х-х0,y-y0,z-z0).
Условие перпендикулярности векторов ×=0 дает искомое уравнение. Ответ получим по
формуле для вычисления скалярного произведения.
Ответ: А(х-х0)+В(y-y0)+С(z-z0)=0
Воспользуемся этим результатом для решения следующего примера:
Написать уравнения плоскости, проходящей
через точку М0(2,-4,3) и перпендикулярной вектору =(1,-2,0).
Ответ: (х-2)-2(у+4)+0(z-3)=0 или х-2у=10.
II. Дано уравнение или система уравнений. Найти геометрический образ, заданный эти уравнением или системой.
Пример:
На плоскости задано уравнение 
. Найти линию, которую описывает это
уравнение.
Решение:
Рассмотрим точки две точки: О (0,0) – начало координат и М(х,у).
=(х,у); 
.
Очевидно, что уравнение равносильно условию: 
. Следовательно, данное уравнение –
уравнение линии, все точки которой расположены на расстоянии 3 от начала координат,
т.е. уравнение окружности 
3.
Ответ: -
окружность 3 с центром в начале координат.
3.8.2 Уравнения некоторых линий и поверхностей.
В пространстве:
Ах+Ву+Сz=D - уравнение плоскости,
вектор =(А,В,С) – перпендикуляр (нормаль) к
плоскости
42
Определитель квадратной матрицы Аnxn также иногда называют минором n-ого порядка данной матрицы.
Например, матрица А=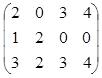
имеет
- четыре минора третьего порядка: эти миноры получаются при вычеркивании любого (одного) столбца;
- восемнадцать миноров второго порядка: эти миноры получаются при вычеркивании одной строки и двух столбцов;
- двенадцать миноров первого порядка: каждый элемент матрицы можно считать минором первого порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.