[F-(j¢-y¢)Fy¢]x=x0=0
[F+(j¢-y¢)Fy¢]x=x0=0П
[F-(j¢-y¢)Fy]x=x0=0
[Fу+(j-y)Fy¢]x=x0=0
- Условие экстремальности в точке отражения экстремали х = х0
имеет вид
[F+(j¢-y¢)Fy¢]x=x0-0
= [F+(j¢-y¢)Fy¢]x=x0+0П
[F-(j¢-y¢)Fy¢]x=x0-0
= [F-(j¢-y¢)Fy¢]x=x0+0
[Fу +(j¢-y¢)Fy¢]x=x0-0
= [Fу+(j¢-y¢)Fy¢]x=x0+0
[Fу+(j-y)Fy¢]x=x0-0 = [Fу+(j-y)Fy¢]x=x0+0
- Условие экстремальности в точке преломления экстремали х =
х0 имеет вид
[F1+(j¢-y¢)F1y¢]x=x0-0
= [F2+(j¢-y¢)F2y¢]x=x0+0П
[F1+(j-y)F1y¢]x=x0-0
= [F2+(j-y)F2y¢]x=x0+0
[F1+(j¢-y¢)F2y¢]x=x0-0
= [F2+(j¢-y¢)F1y¢]x=x0+0
[F1у+(j¢-y¢)F1y¢]x=x0-0 = [F2у+(j¢-y¢)F2y¢]x=x0+0
- Условие Якоби для экстремалей функционала
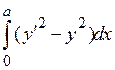
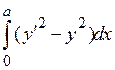 ,
проходящих через точки (0, 0) и (а, 0):
,
проходящих через точки (0, 0) и (а, 0):
выполнено для всех а
не выполнено для любых а
выполнено для 0<а<pП
выполнено для a³p
- Функция Вейерштрасса E(x, y, p,
y¢)
для функционала
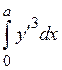 имеет вид
имеет вид
(y¢-p)2(y¢+2p)П
(y¢+p)2(y¢+p)
(y¢-2p)2(y¢+p)
(y¢-2p+py)2
- Условие Лежандра для функционала
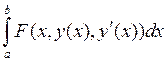 имеет
вид
имеет
вид
Fyy³0 (Fyy£0)
Fyy¢³0 (Fyy¢£0)
Fxy³0 (Fxy£0)
Fy¢y¢³0 (Fy¢y¢£0)П
- Экстремаль функционала
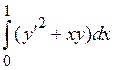 ,
у(0)=у(1)=0 имеет вид
,
у(0)=у(1)=0 имеет вид
у(х) = sinpx
y(x)=x(1-x2)
y(x) = (x3-x)/12П
y(x) = x(1-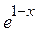 )
)
- Экстремаль функционала
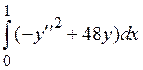 ,
удовлетворяющая условиям у(0)=у¢(0)=0,
y(1)=1, y¢(1) = 4, имеет вид
,
удовлетворяющая условиям у(0)=у¢(0)=0,
y(1)=1, y¢(1) = 4, имеет вид
у=х4П
у=х2+2(1-х)2
у=(1-х)4+4(1-х)+6х2
у=х3-х2
- Прямые методы решения задач вариационного исчисления
основаны на
представлении экстремалей в виде
ломанной линии
представлении экстремалей в виде
семейства прямых линий
замене вариационной задачи
задачей на экстремум функции нескольких переменныхП
замене вариационной задачи
дифференциальным уравнением
- Метод Ритца заключается приближенном представлении
экстремали функционала в виде
отрезка тригонометрического ряда
Фурье
многочлена с неизвестными
коэффициентами по степеням независимой переменной
линейной комбинации базисных
функций с неизвестными коэффициентамиП
подходящей дробно-рацинальной
функции
- Экстремалью функционала
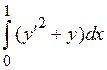 ,
у(1)=0 является
,
у(1)=0 является
у(х) =1-х
у(х) = (х2-1)/4П
у(х) =1-х2
у(х) =х2-4х+3
- Уравнение
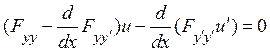 называется
уравнением
называется
уравнением
Эйлера-Пуассона
Эйлера
ЯкобиП
Вейерштрасса
Вопросы к экзамену
- Оптимизация функции одного
переменного.
- Необходимые и достаточные
условия экстремума.
- Общая характеризационная
теорема.
- Необходимые условия экстремума
функции нескольких переменных.
- Достаточные условия второго
порядка. Матрица Гессе.
- Условная оптимизация при наличии
ограничений типа равенств.
- Метод множителей Лагранжа.
- Одномерная оптимизация. Метод
Фибоначчи.
- Метод золотого сечения.
- Методы покоординатного спуска
- Метод Хука и Дживса
- Метод Розенброка.
- Метод градиентного спуска.
- Метод наискорейшего спуска.
- Метод сопряженных градиентов.
- Элементы выпуклого анализа.
Выпуклые множества. Выпуклые функции. Критерии выпуклости.
- Дифференцируемость выпуклых
функций.
- Субградиент и его свойства.
- Метод штрафных функций.
Сходимость метода штрафных функций.
- Метод проекции градиента.
- Метод условного градиента.
- Вариация функции и ее свойства.
- Уравнения Эйлера.
- Основная лемма вариационного
исчисления.
- Уравнения Эйлера для
функционалов, зависящих от функций нескольких переменных.
- Функционалы, зависящие от
производных высших порядков и условия их экстремума.
- Экстремумы функционалов,
зависящих от функций нескольких переменных.
- Параметрические задачи.
- Сильный и слабый экстремум.
- Задачи с подвижными границами.
- Условия трансверсальности.
- Экстремали с угловыми точками.
- Преломление экстремалей.
- Односторонние вариации.
- Поле экстремалей. Уравнение
Якоби.
- Функция Вейерштрасса. Условие
Вейерштрасса.
- Условие Лежандра.
- Вариационные задачи на условный
экстремум. Неголономные и голономные связи.
- Метод Эйлера.
- Метод Ритца.
- Метод Канторовича.
- Постановка задач оптимального
управления. Задача Майера.
- Игольчатая вариация.
- Принцип максимума Понтрягина.
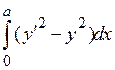
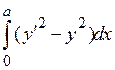 ,
проходящих через точки (0, 0) и (а, 0):
,
проходящих через точки (0, 0) и (а, 0):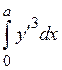 имеет вид
имеет вид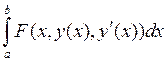 имеет
вид
имеет
вид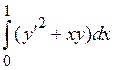 ,
у(0)=у(1)=0 имеет вид
,
у(0)=у(1)=0 имеет вид![]() )
)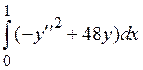 ,
удовлетворяющая условиям у(0)=у¢(0)=0,
y(1)=1, y¢(1) = 4, имеет вид
,
удовлетворяющая условиям у(0)=у¢(0)=0,
y(1)=1, y¢(1) = 4, имеет вид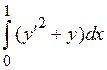 ,
у(1)=0 является
,
у(1)=0 является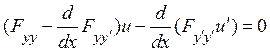 называется
уравнением
называется
уравнением