Указанное преобразование можно
выполнить, если рекуррентная функция ![]() является
полуассоциативной, то есть для нее выполняется следующее соотношение:
является
полуассоциативной, то есть для нее выполняется следующее соотношение:
![]() , (2.6)
, (2.6)
где ![]() – некоторая
сопровождающая функция.
– некоторая
сопровождающая функция.
Для полуассоциативной рекуррентной функции f с сопровождающей функцией g выполняется такое соотношение:
![]() , (2.7)
, (2.7)
то есть, рекурсивная подстановка выполняется для сопровождающей функции g с применением ассоциативной расстановки скобок.
Если применить названные свойства
(2.6, 2.7) к рекуррентному выражению ![]() , то следующие значения
последовательности x можно представить так:
, то следующие значения
последовательности x можно представить так:
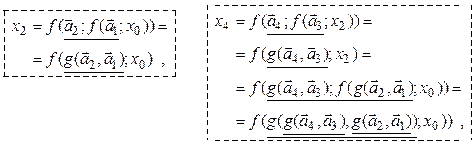
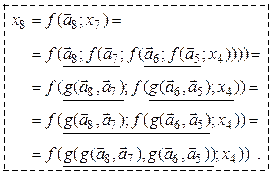
Подставив вместо ![]() его рекуррентную функцию, будем далее
иметь:
его рекуррентную функцию, будем далее
иметь:
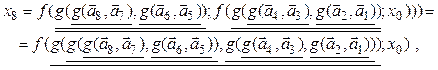
Аналогичным образом можно описать
параллельную форму для получения члена рекуррентной последовательности ![]() Основной операцией, выполняемой над парами
исходных и промежуточных данных, служит сопровождающая функция
Основной операцией, выполняемой над парами
исходных и промежуточных данных, служит сопровождающая функция ![]() . В развернутых формулах промежуточные
значения разных уровней сдваивания подчеркнуты отрезками линий. Параллельная
форма будет выглядеть так, как показано на рисунке 2.4а, если предположить, что
каждый кружок со знаком плюс, представляет преобразование, выполняемое
сопровождающей функцией.
. В развернутых формулах промежуточные
значения разных уровней сдваивания подчеркнуты отрезками линий. Параллельная
форма будет выглядеть так, как показано на рисунке 2.4а, если предположить, что
каждый кружок со знаком плюс, представляет преобразование, выполняемое
сопровождающей функцией.
Определенную сложность представляет задача нахождения вида сопровождающей функции для заданного рекуррентного выражения в случае, когда рекуррентная функция является нелинейной. При этом часто необходимо прикладывать все свои интеллектуальные способности и математические знания, чтобы выделить рекурсивное операционное ядро в заданном рекуррентном выражении.
В качестве примера рассмотрим
следующее нелинейное рекуррентное выражение первого порядка, возникающее при ![]() -разложении трехдиагональной матрицы:
-разложении трехдиагональной матрицы:
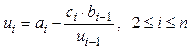 .
.
Здесь ![]() векторные элементы,
входящие в исходные и результирующие матрицы. Для устранения операции деления
умножим левую и правую часть рекуррентного выражения на
векторные элементы,
входящие в исходные и результирующие матрицы. Для устранения операции деления
умножим левую и правую часть рекуррентного выражения на ![]() :
:
![]() .
.
Введем новую рекуррентно
вычисляемую переменную ![]() , связанную с искомой
рекуррентной последовательностью, следующим образом:
, связанную с искомой
рекуррентной последовательностью, следующим образом:
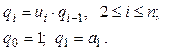
После замены переменных в исходном выражении, получим
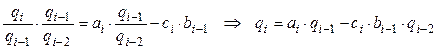 .
.
В результате преобразований имеем линейную рекуррентную функцию второго порядка, которую удобно представить в матричной форме:
![]() ,
,
где 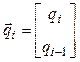 и
и 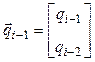 – двухкомпонентные векторы;
– двухкомпонентные векторы;
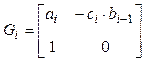 – матрица из
параметров выражения.
– матрица из
параметров выражения.
Развернутое матричное рекуррентное выражение будет иметь вид
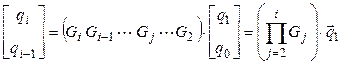 .
.
Для развернутого произведения
матрицы из заранее известных параметров могут вычисляться параллельно. Так как
произведение матриц ассоциативно, то при вычислении можно использовать метод
сдваивания. Рисунок 2.4а дает представление об этой параллельной форме
вычислений, если полагать, что операции, помеченные в этой форме знаком плюс,
являются операциями произведения матриц ![]() .
.
Здесь уместно отметить затраты
времени на выполнение произведения матриц ![]() ,
которое для сохранения структуры алгоритма сдваивания должно вычисляться на
одном процессоре.
,
которое для сохранения структуры алгоритма сдваивания должно вычисляться на
одном процессоре.
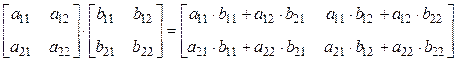
Скалярная арифметика на
вычисление одной компоненты матрицы ![]() требует два умножения и
одно сложение, поэтому на произведение матриц необходимо затратить
требует два умножения и
одно сложение, поэтому на произведение матриц необходимо затратить ![]() операций. Если в арифметико-логическом
устройстве процессора аппаратно реализовано скалярное произведение векторов, то
на вычисление произведения матриц
операций. Если в арифметико-логическом
устройстве процессора аппаратно реализовано скалярное произведение векторов, то
на вычисление произведения матриц ![]() потребуется всего 4
скалярных умножения:
потребуется всего 4
скалярных умножения:
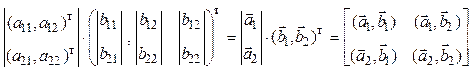
Учитывая сказанное относительно
числа операций на реализацию умножения матриц ![]() ,
отметим, что глубина параллельной формы для вычисления матричной рекурсии
второго порядка скалярными однотактными арифметическими операциями увеличится в
12 раз, а векторными – в 4 раза.
,
отметим, что глубина параллельной формы для вычисления матричной рекурсии
второго порядка скалярными однотактными арифметическими операциями увеличится в
12 раз, а векторными – в 4 раза.
Возможность выполнения
однотактных векторных операций в процессорах и параллельный обмен векторными
данными открыл бы дорогу для увеличения матричных вычислений в число раз,
равное размерности векторов. В этом случае векторные рекуррентные вычисления
высоких порядков тоже можно было бы сводить к рассмотренной выше схеме
сдваивания, но с матрицами ![]() и векторами размерности
n , например, при заданных векторах
и векторами размерности
n , например, при заданных векторах ![]() , рекурсия четвертого порядка
, рекурсия четвертого порядка
![]() , (2.8)
, (2.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.