Приведение системы сил к простейшей системе

§ 1.5. Приведение системы сил к простейшей системе

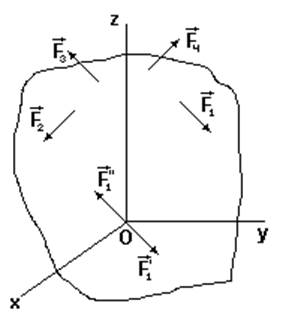            Пусть на тело действует система сил .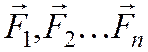

Приведем систему сил к заданному центру (докажем теорему Пуансо). Выберем произвольную точку О за точку приведения. Рассмотрим одну из сил системы – F₁. Добавим в точке О нулевую систему сил – (F₁',F₁") ( |F₁| = |F₁'| = |F₁"| ). Заметим, что силы (F₁,F₁") представляют пару сил, которую можно заменить вектором момента пары M₀(F₁), приложенным в точке  О (он же равен моменту силы F₁ относительно центра О), т.е. исходная сила эквивалентна силе F₁' и вектору момента пары, обе приложены в точке О.

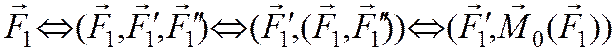
            Проведя аналогичную операцию со всеми векторами исходной системы сил мы получим два пучка векторов, приложенных в точке О – пучок сил 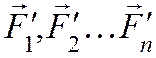 и пучок векторов моментов 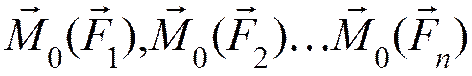, которые приводятся к эквивалентной системе двух векторов:

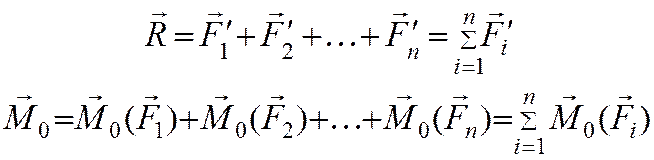
            Главным вектором системы сил называют вектор, равный векторной сумме этих сил (вектор равнодействующей R).

Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки (вектор момента результирующей пары М₀). Вектор М₀ зависит от точки приведения О.

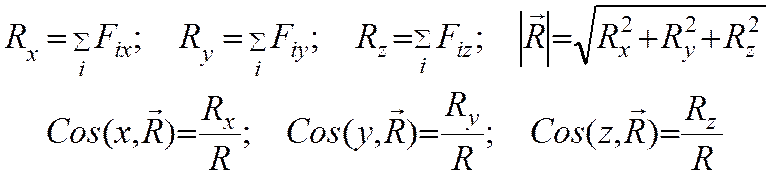
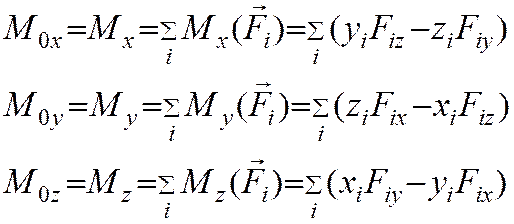
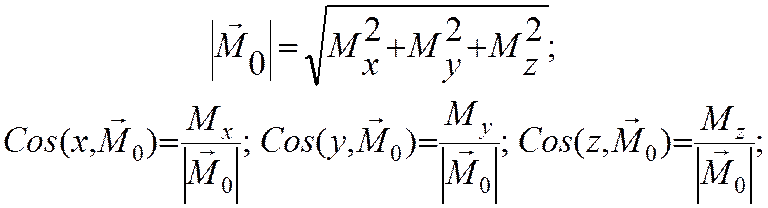
§ 1.6. Условия равновесия систем сил

Пространственная система сил

Если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из равнодействующей и результирующего момента пары. Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно, чтобы

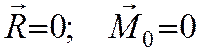 (для любой точки О)

            Эти условия являются векторными условиями равновесия для любой системы сил. В аналитической форме это эквивалентно R_x=R_y=R_z=0; M_x=M_y=M_z=0, т.е. в самом общем случае имеем шесть скалярных уравнений равновесия.

Пространственная система параллельных сил

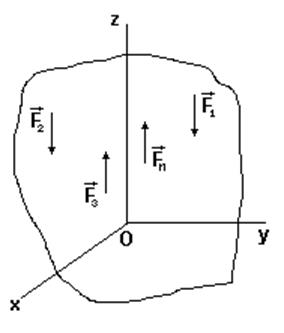
­­ Oz, т.е. ­­

M_z тождественно равно нулю,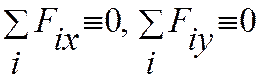

Имеем в итоге три уравнения:

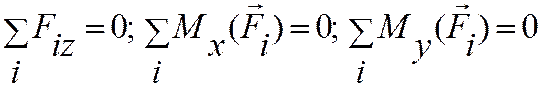
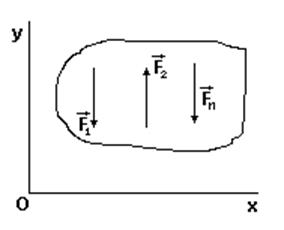
Плоская система сил

После отбрасывания тождеств

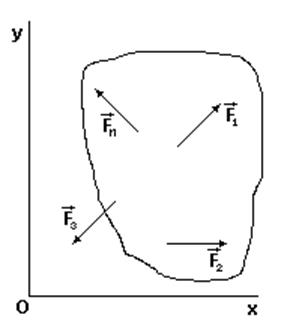
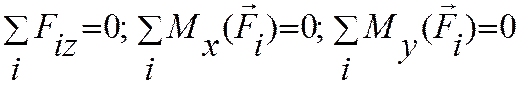
имеем три уравнения

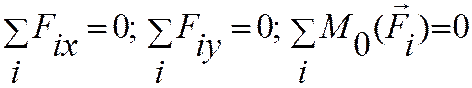 (для любой точки)

            Для плоской системы параллельных сил имеем два уравнения равновесия:

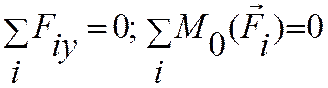 (для любой точки)

Теорема о моменте равнодействующей силы (теорема Вариньона)

            Пусть система сил не находится в равновесии и может быть приведена к равнодействующей .

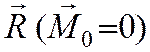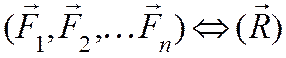
            Добавим к этой системе сил , тогда

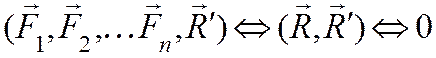
            Эта новая система сил, эквивалентная нулю, удовлетворяет условиям равновесия системы сил и, в частности, условию равенства нулю суммы векторных моментов сил относительно любой точки:

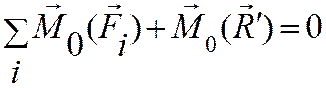
            Т.к. 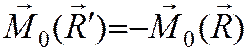, то имеем теорему Вариньона

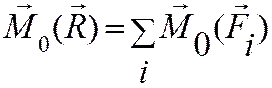
            Это справедливо и в любых проекциях, например 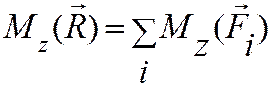, т.е. для плоской системы сил имеем теорему Вариньона в алгебраических моментах

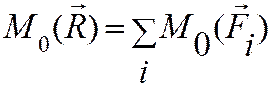
            Различные формы условий равновесия плоской системы сил:

1. Ранее приведенная форма условий -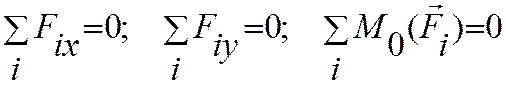  

2. Эквивалентная ей система уравнений равновесия

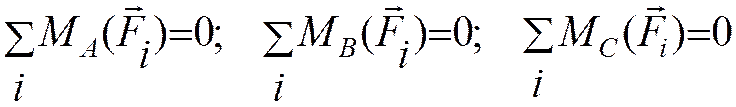
для любых трех точек, не лежащих на одной прямой.

3. Также эквивалентная первой система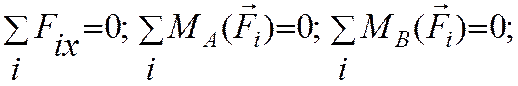

для любых точек А и В, если ось х не перпендикулярна отрезку АВ.

Для равновесия плоской системы параллельных сил имеем альтернативную форму условий равновесия 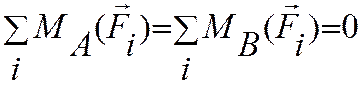 для любых точек А и В:

Статически определимые и неопределимые задачи

            Для любой системы сил для разрешимости задач необходимо, чтобы число неизвестных сил не превышало максимального числа возможных уравнений равновесия. Такие задачи называют статически определимыми. В противном случае задача статически неопределима в рамках моделей твердых тел.

Равновесие системы тел

            При рассмотрении равновесия системы сил, приложенных к системе нескольких взаимодействующих между собой тел, мысленно расчленяем систему на части и внутренние силы для части считаем внешними силами. Внутренние силы образуют по аксиоме о взаимодействии равновесную систему ().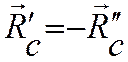

§1.7. Внутренние напряжения в конструкциях

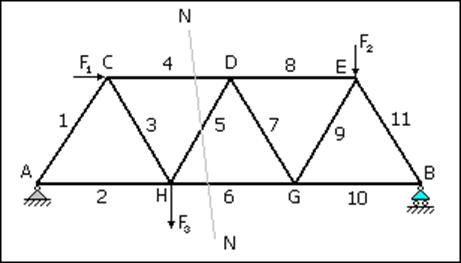            Рассмотрим ферму – плоскую жесткую конструкцию, состоящую из стержней, соединения стержней шарнирные. К ферме приложены внешние сосредоточенные нагрузки F₁, F₂ и F₃. Необходимо определить, с какой силой сжаты или растянуты все стержни фермы. Это типовая задача для инженерного расчета на прочность строительных конструкций (фермы опор линий электропередач, мосты и пр.)

            Ферма в точке А закреплена в шарнире в точке В – опора. Существует ряд методов для решения этой задачи. На первом этапе применения всех методов необходимо рассмотреть конструкцию как единое целое, находящееся под действием заданных нагрузок, и определить внешние реакции (для нашего случая это реакция шарнира А и опоры В). В некоторых частных случаях результаты этого этапа могут не влиять на значения напряжений в некоторых стержнях, однако при определении напряжений во всех стержнях фермы внешние реакции требуется определять.

            Чаще используются два метода: метод вырезания узлов и метод Риттера.

            а) метод вырезания узлов заключается в последовательном мысленном вырезании узлов и рассмотрения условий их равновесия. Все стержни фермы считаем сжатыми. Тогда при рассмотрении равновесия узла действие разрезанных стержней на узел заменяем реакциями, направленными к узлу. Так для нашего случая для узла А будем иметь задачу: