Принцип Даламбера. Движение точки по поверхности. Движение точки по линии

§3.14 Принцип Даламбера

            Принцип Даламбера удобен для рассмотрения систем со связями (несвободных систем) и позволяет уравнениям динамики придать форму уравнений статики.

          Принцип Даламбера для материальной точки.

Уравнение движения точки запишем в виде 2-го закона Ньютона : , где - равнодействующая активных сил, действующих на точку, а - равнодействующая реакций связей, наложенных на точку.

Назовем силой инерции материальной точки величину , тогда уравнение движения перепишется в виде:

            Это и есть принцип Даламбера для материальной точки: “При движении материальной точки активные силы и реакций связей вместе с силой инерции точки образуют равновесную систему сил”.

          Принцип Даламбера для системы материальных точек.

Для каждой точки, входящей в материальную систему имеем принцип Даламбера:

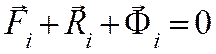 (i=1,2…n), где 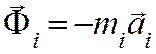-сила инерции i-ой точки.

Проводя суммирование по всем точкам материальной системы получим принцип Даламбера для системы точек “При движении механической системы активные внешние  силы и реакции внешних связей вместе с силами инерции точек составляют равновесную систему сил”:

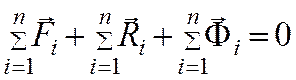
          Силы инерции твердого тела.

При поступательном движении твердого тела ускорение всех его точек одинаковы. Система сил инерции приводится к равнодействующей силе 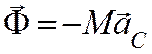. Линия действия этой равнодействующей проходит через центр масс системы.

При вращении твердого тела вокруг неподвижной оси с угловой скоростью w и угловым ускорением e каждая точка имеет ускорение 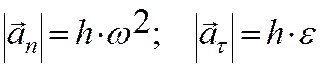  (здесь h - расстояние точки до оси вращения). Нормальное ускорение a_n направлено к оси вращения, тангенциальное ускорение a_t перпендикулярно радиусу вращения каждой точки и направление его зависит от знака углового ускорения. Для каждого конкретного случая необходимо построить эпюру сил инерции точек тела и найти равнодействующую силу инерции. Равнодействующая будет равна произведению массы тела на ускорение центра масс. Линия действия равнодействующей проходит через центр тяжести эпюры этих распределенных сил инерции.

В качестве иллюстрации применения принципа Даламбера для решения задач рассмотрим следующий пример.

Груз А силой тяжести Р1 опускается вниз по грани призмы с силой тяжести Р приводя в движение груз В, имеющий силу тяжести Р2. Призма с углами a и b при основании находится на горизонтальной плоскости (ось x), ее движение влево ограничивает вертикальная стенка (ось y). Трение отсутствует. Найти реакцию горизонтальной плоскости N, реакцию вертикальной плоскости F и силу натяжения нити T.

Предположим, что груз А движется с ускорением a. Силы инерции грузов будут равны

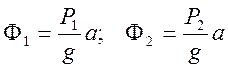
Применим к системе принцип Даламбера:

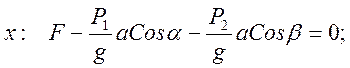
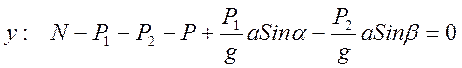
Из этих уравнений имеем:

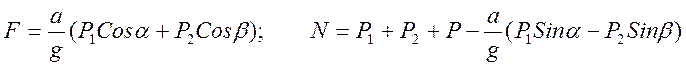
Для определения T и a применим принцип Даламбера к каждому грузу в отдельности, составив условия равновесия внешних сил грузов и сил инерции в проекции на направление нити:

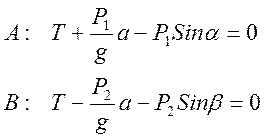              è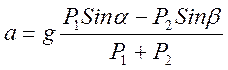               

Отсюда видно, что для того, чтобы груз А двигался вниз, ускорение a должно быть больше нуля, то есть P₁Sina > P₂Sinb.

Подставляя результат для a в выражения для F и N получим:

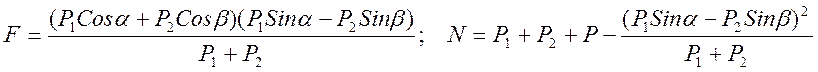
Для натяжения нити T можно также получить:

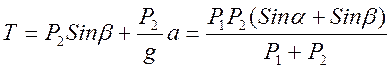
§3.15 Движение точки по поверхности

          Рассмотрим задачу о движении точки по поверхности.

Точка движется по поверхности, заданной уравнением f(x,y,z)=0 (это уравнение является уравнением связи для точки), на точку действует внешняя сила F. Считаем поверхность гладкой, поэтому реакция поверхности N нормальна к поверхности. Необходимо найти закон движения точки по поверхности и реакцию поверхности.

            Составим для точки уравнения движения в форме второго закона Ньютона:

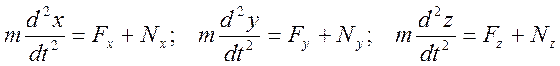
            Из дифференциальной геометрии известно, что направляющие косинусы к внешней нормали поверхности, а тем самым и к N, вычисляются следующим образом:

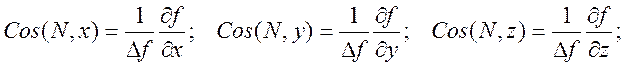
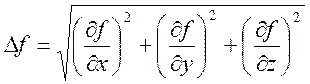
Таким образом, компоненты реакции N можно представить в виде:

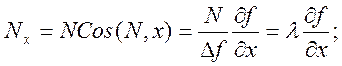
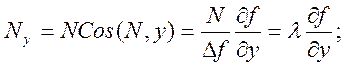
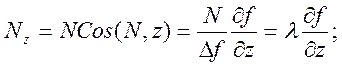
            Окончательно имеем уравнения движения в виде:

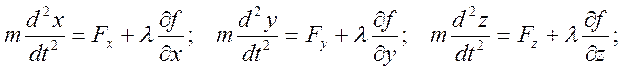
            Добавив к ним уравнение поверхности f(x,y,z)=0 получим систему трех обыкновенных дифференциальных уравнений и одно алгебраическое уравнение для определения четырех неизвестных величин x(t), y(t), z(t), l(t). После определения величины l можно найти значение реакции N=lDf.

§3.16 Движение точки по линии

            Рассмотрим задачу о движении точки по линии.

Точка движется по линии, которая задается пересечением двух поверхностей f1(x,y,z)=0 и f2(x,y,z)=0, на точку действует внешняя сила F. Считаем линию гладкой, поэтому реакция линии N нормальна к линии. Необходимо найти закон движения точки по линии и реакцию линии.

            Разложим реакцию линии  N на две составляющие, каждая из которых нормальна к своей поверхности:

            Составим для точки уравнения движения в форме второго закона Ньютона:

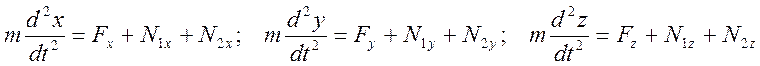
            Для каждой из составляющих N₁ и N₂ (как это было сделано в задаче о движении точки по поверхности) найдем направляющие косинусы:

;   

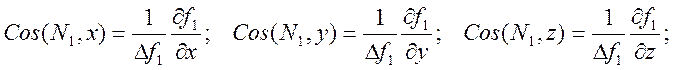
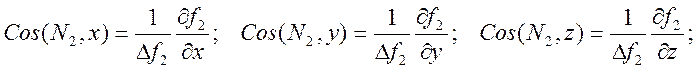
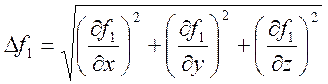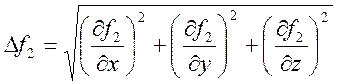
Компоненты реакций N₁ и N₂  теперь можно представить в виде:

         

         

         

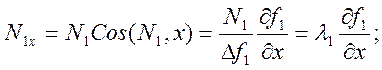
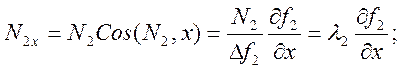
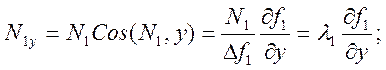
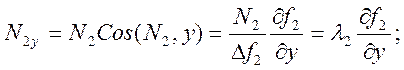
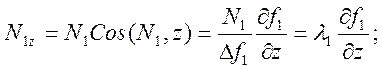
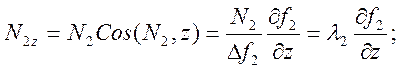
          Окончательно имеем уравнения движения точки по линии в виде:

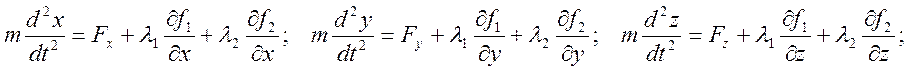 (3.16.1)

            Добавив к ним уравнения поверхностей f₁(x,y,z)=0 и f₂(x,y,z)=0 получим систему трех обыкновенных дифференциальных уравнений и двух алгебраических уравнений для определения пяти неизвестных величин x(t), y(t), z(t), l₁(t), l₂(t). После определения величин l₁ и l₂ можно найти значения реакций N₁=l₁Df₁ и N₂=l₂Df₂.