![]() . (2.8)
. (2.8)
В этом случае вторым членом в левой части (2.6) также пренебрегают, и уравнение притока тепла записывается в виде
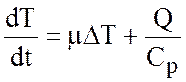 ,
,
где 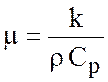 -
коэффициент температуропроводности. С учетом соотношения (2.8) в последнем
уравнении температуру можно заменить плотностью, что приводит к уравнению
-
коэффициент температуропроводности. С учетом соотношения (2.8) в последнем
уравнении температуру можно заменить плотностью, что приводит к уравнению
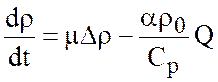 . (2.9)
. (2.9)
Важно отметить, что уравнения (2.2) и (2.9) представляют собой два разных физических закона: первое уравнение выражает закон сохранения массы, второе выражает закон сохранения внутренней энергии.
2.2. Уравнения движения во вращающейся системе координат.
Мы вывели систему уравнений в
инерциальной системе координат, с наблюдателем, находящимся вне вращающейся
системы координат. Это является наиболее полным описанием перемещение частицы в
пространстве. Однако, часть этого движения не является определяющей для
движений на вращающейся планете. Поэтому наиболее естественной является
система координат вращающаяся с угловой скоростью ![]() (
(![]() - вектор угловой скорости вращения Земли).
- вектор угловой скорости вращения Земли).
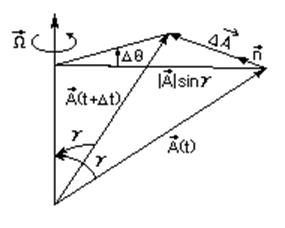
Рис. 2.1.
Рассмотрим постоянный вектор ![]() , который вращается с угловой скоростью
, который вращается с угловой скоростью ![]() . Угол между векторами
. Угол между векторами ![]() и
и ![]() равен
равен ![]() . За малое время
. За малое время ![]() вектор
вектор
![]() повернется на угол
повернется на угол 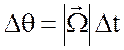 .
За этот период вреени изменение
.
За этот период вреени изменение ![]() равно (Рис. 2.1)
равно (Рис. 2.1)
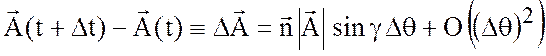 ,
,
где ![]() -
единичный вектор в направлении изменения
-
единичный вектор в направлении изменения ![]() ,
который перпендикулярен векторам
,
который перпендикулярен векторам ![]() и
и ![]() . Тогда вектор
. Тогда вектор ![]() можно
представить в виде нормированного векторного произведения
можно
представить в виде нормированного векторного произведения
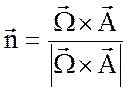 .
.
Переходя к пределу при ![]() приходим к дифференциальному соотношению
приходим к дифференциальному соотношению
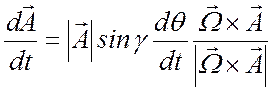 .
.
Для модуля векторного произведения справедлива формула
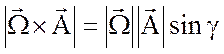 .
.
Тогда окончательно для фиксированного вектора ![]() в невращающейся системе координат имеем выражение
в невращающейся системе координат имеем выражение
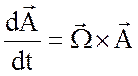 . (2.10)
. (2.10)
Рассмотрим далее произвольный
вектор ![]() в системе координат, вращающейся с угловой
скоростью
в системе координат, вращающейся с угловой
скоростью ![]() . Предположим, что эта система координат
декартова с единичными ортами
. Предположим, что эта система координат
декартова с единичными ортами ![]() . Тогда вектор
. Тогда вектор ![]() может быть представлен в виде
может быть представлен в виде
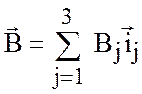 ,
,
где 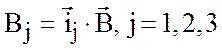 .
Скорость изменения вектора
.
Скорость изменения вектора ![]() со временем для
наблюдателя, находящегося во вращающейся системе отсчета, есть
со временем для
наблюдателя, находящегося во вращающейся системе отсчета, есть
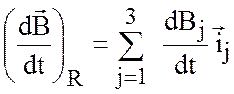 ,
,
где индекс ![]() означает
скорость изменения во вращающейся системе отсчета. В неподвижной системе
отсчета и компоненты вектора
означает
скорость изменения во вращающейся системе отсчета. В неподвижной системе
отсчета и компоненты вектора ![]() , и единичные орты
меняются со временем. Скорости изменения скалярных компонент
, и единичные орты
меняются со временем. Скорости изменения скалярных компонент ![]() одинаковы в обеих системах отсчета,
следовательно,
одинаковы в обеих системах отсчета,
следовательно,
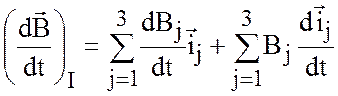 , (2.11)
, (2.11)
где индекс ![]() означает
скорость изменения для наблюдателя в неподвижной (инерциальной) системе
отсчета. Применение (2.10) к каждому из трех единичных векторов дает
означает
скорость изменения для наблюдателя в неподвижной (инерциальной) системе
отсчета. Применение (2.10) к каждому из трех единичных векторов дает
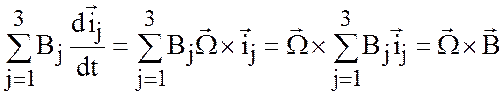 ,
,
так что (2.11) принимает вид
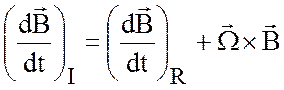 . (2.12)
. (2.12)
Рассмотрим далее ![]() -
радиус-вектор некоторой жидкой частицы. В соответствии с формулой (2.12), скорость
изменения вектора
-
радиус-вектор некоторой жидкой частицы. В соответствии с формулой (2.12), скорость
изменения вектора ![]() в инерциальной системе координат
имеет вид
в инерциальной системе координат
имеет вид
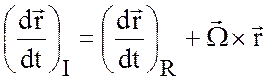 .
.
Поскольку изменения радиус-вектора ![]() со
временем есть скорость
со
временем есть скорость ![]() , то получаем
, то получаем
![]() , (2.13)
, (2.13)
где ![]() называется
относительной скоростью. Применяя (2.12) к
называется
относительной скоростью. Применяя (2.12) к ![]() , имеем
, имеем
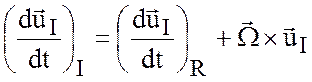 . (2.14)
. (2.14)
Так как нам необходимо описать движение,
используя лишь величины, наблюдаемые во вращающейся системе отсчета, перепишем
(2.14), исключив из него ![]() при помощи (2.13),
при помощи (2.13),
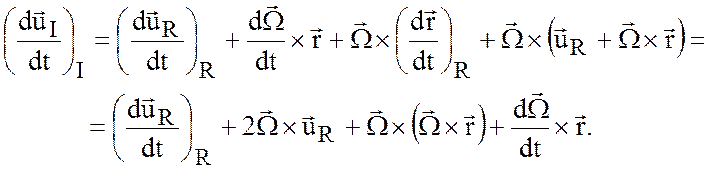 (2.15)
(2.15)
Таким образом, изменения,
происходящие при переходе от невращающейся к вращающейся системе отсчета, определяется
суммой трех членов в правой части (2.15). Это ускорение Кориолиса ![]() , центростремительное ускорение
, центростремительное ускорение ![]() и ускорение, обусловленное изменениями
самой скорости вращения.
и ускорение, обусловленное изменениями
самой скорости вращения.
Последнее из этих слагаемых изучаемых процессов
можно не учитывать, считая ![]() постоянной.
постоянной.
Центростремительное ускорение может быть
выражено через потенциальную функцию ![]()
![]() ,
,
где
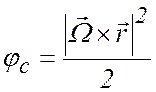
Теперь
центростремительная сила может быть включена в общий потенциал ![]() .
.
Необходимо отметить, что хотяполная производная скалярной величины одна и та же в обеих системах
отсчета, отдельные ее компоненты не инварианты. В частности, для любой
скалярной величины ![]() можно показать, что
можно показать, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.