Первая и вторая теоремы Вейерштрасса. Теория локального экстремума. Аксиомы вещественных чисел, страница 4

Теоремы о пределах:

Теорема 1: если последовательность имеет конечный предел, то он один.

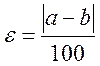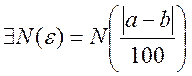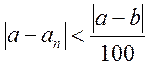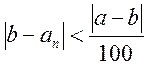Доказательство: допустим, что имеет два предела, тогда и , причем . Возьмем . Тогда , что выполняется и . Тогда 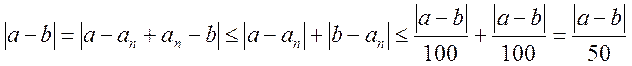, т.е. 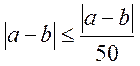, что верно => предел, единственный.

Теорема 2: если последовательность имеет конечный предел, то она ограничена, т.е. и , что .

Доказательство: для , (по определению). Рассмотрим верхняя граница => для . Возьмем нижняя граница =>

Теорема 3: если ,и ,и (существует конечный предел и ). Тогда

Доказательство: пусть , возьмем ,

Для

Возьмем , т.е. 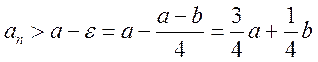, , 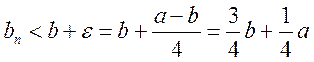т.е. , что противоречит.

Теорема 4: если , то

Доказательство: , , при , при

Теорема 5: если 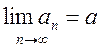и и 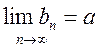, тогда

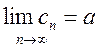
Доказательство: ;

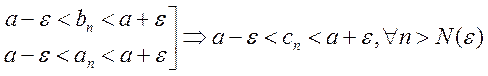
Теория локального экстремума.

Теорема 1(необходимое условие экстремума): если функция - непрерывна на и в точке имеет экстремум. Тогда, если

Доказательство: будем считать, что - точка максимума (т.е. ), . Тогда - точка . По теорема Ферма . - это стационарные точки () – подозрительные на экстремум.

Теорема 2: пусть - непрерывна на и при переходе через точки функция меняет знак, тогда в точке экстремум: , если при и при и , если при и при .

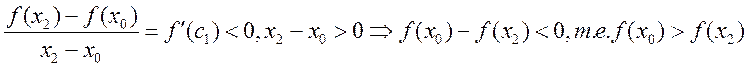Доказательство: на промежутке ,- непрерывна и на произв. - ; где

; где - точка

Теорема 3 (достаточное условие экстремума): пусть функция дважды непрерывно дифференцируемая на и пусть точка обладает свойствами: 1) ; 2) . Тогда в точке - экстремум , если и , если

Доказательство: т.к. непрерывна разлагается в строку Тейлора: 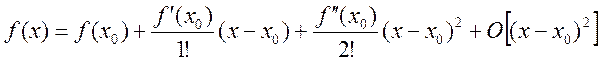, т.е. 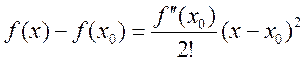, где , т.к. если . Найдется окр. точки , где . тоже непрерывна в некоторой окрестности точки

Теорема 4: пусть функция раз непрерывно дифференцируемая на и пусть , что 1) ; 2) . Тогда если четное число, то - точка экстремума. Если же - нечетное число экстремума нет в точке .

Доказательство: по формуле Тейлора:

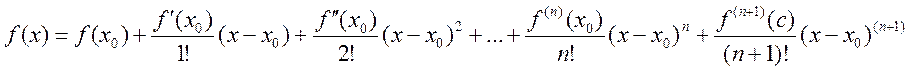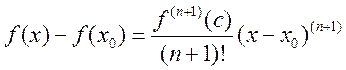, . По условию , - непрер. будет сохранять знак в окрестности точки , т.е. в окрестности точки , в част. – точки с. Тогда совпадает со знаком . 1) если (n+1) – четное . А если 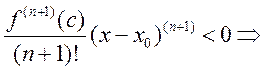.2) если (n+1) - нечетноевеличина меняет знакнет экстремума.

Формула Лейбница для вычисления n-производной

Формула Лейбница: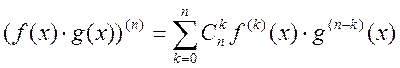

Утверждение: пусть и имеют производные n – порядка. Тогда имеет место формула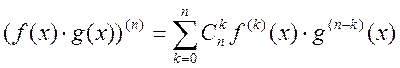

Доказательство по инд.: 1) n=1 - да, верно.2) док-жем, что для (m+1) – верно, предположив, что для m – верно ;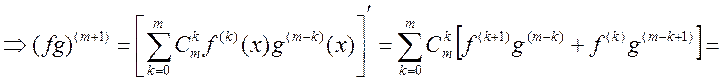

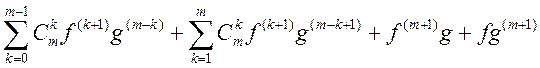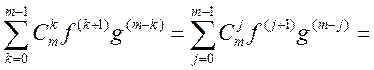
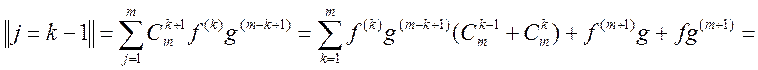
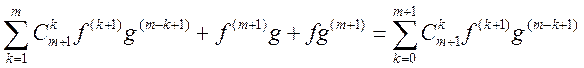. Ч.т.д.

Формула Ньютона – Лейбница.

Теорема: пусть непрерывна на , тогда для существует первообразная , т.е. . Для любой первообразной справедливо равенство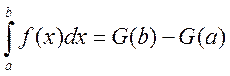

Доказательство: функция 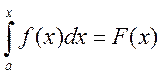является первообразной. Имеем след. равенство: 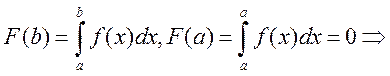вычитаем 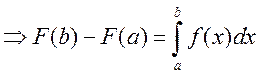. Возьмем любую первообразную, пусть - некоторая первооб. что . .ч.т.д.

Формула Тейлора с остатками

Теорема: Пусть функция (n+1) раз непрерывно диф-ма в окрестности точки . Тогда в этой окрестности имеет место формула Тейлора 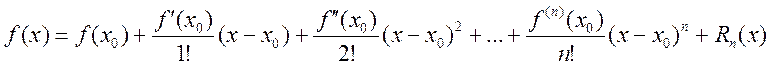, где - остаток: 1) , где с- некоторая точка , p – некоторая точка, p>0. 2) - остаток в форме Коши. 3) - остаток в форме 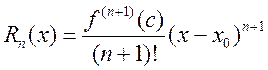Лагранжа. 4) - остаток в форме Пеано

Доказательство: фиксируем x, и рассмотрим функцию ,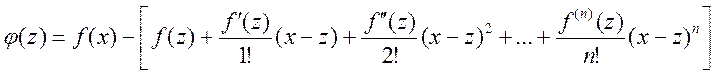

1) 2) 3); ; ;

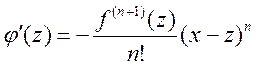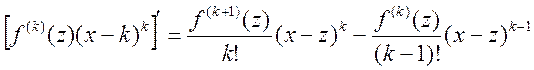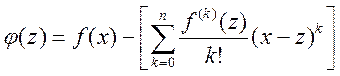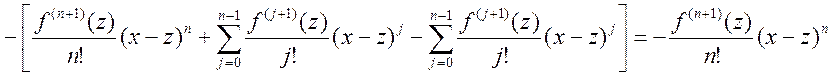
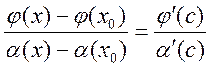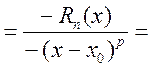
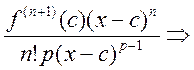
Теперь выведем функцию , где , - фикс. . Свойства: 1) ; 2) ; эта функция непрерывна в отк. Промежутке, диф. в обратном, Þ применим формулу Коши , где . Подставляем Þ слева справа. Теперь получим формы Коши, Лагранжа и Пеона:

1) p=1 - остаток в форме Коши

2) p=1+n - остаток в форме Лагранжа

3) в форме Пеано: функция непрерывна в окрестности x₀ => будет ограничена (по теореме Вейерштрасса) => поделили на . Формула доказана.

Представление остатка в формуле Тейлора в интегральном виде: пусть непрерывно диф-ая (n+1) раз, . Тогда справедливо равенство

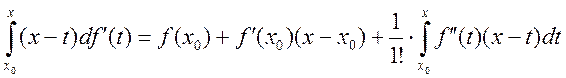Доказательство: индукция по n 1) n=0 2) n=1 3)

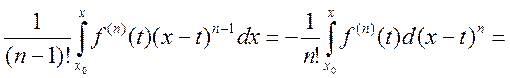
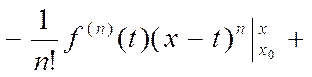
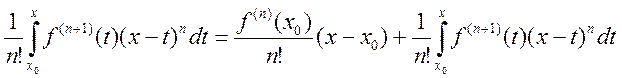
Числовая последовательность:

если для каждого натурального числа n определено некоторое правило сопоставляющее ему число x_n, то множество чисел х₁,х₂, … ,х_n, … называется числовой последовательностью и обозначается {x_n}, причем числа образующие данную последовательность называются ее элементами, а элемент х_n общим элементом последовательности.

1 2 3 4

Скачать файл