Однородное линейное уравнение. Неоднородные уравнения, страница 2

Если частное решение подобрать затруднительно, для нахождения общего решения НЛДУ (обычно) применяют метод вариации произвольных постоянных (метод Лагранжа), который всегда дает возможность найти общее решение уравнения (6.1), если известна фундаментальная система решений соответствующего ему ОЛДУ (6.2). Этот метод заключается в том, что решение (6.1) ищется в том же виде, что и ОЛДУ:

                                                                  (6.8)

где  - некоторые непрерывно дифференцируемые функции от x, подлежащие определению. Эти функции определяются из системы:

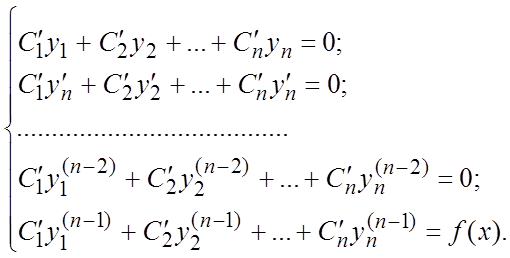                                                       (6.9)

Решая систему (6.9) как алгебраическую, находят производные  от искомых функций; далее интегрированием восстанавливают и сами эти функции.

Пример 8. Зная, что функци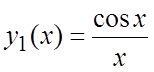и  и 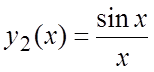 образуют фундаментальную систему решений ОЛДУ 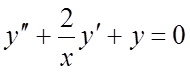 (см. задачу 27), найти общее решение уравнения .

Решение. 1. Общее решение соответствующего ОЛДУ запишем в виде (6.3): 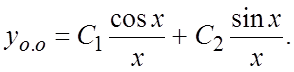 2. Найдем общее решение НЛДУ. а) нетрудно в данном случае подобрать частное решение: y =1. По формуле (6.7) записываем обще решение: 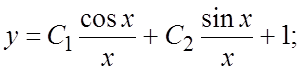 б) найдем общее решение НЛДУ по методу вариации произвольных постоянных (формула (6.8)), для чего составим систему (6.9) (исходное уравнение следует привести к виду (6.1), поделив его на x):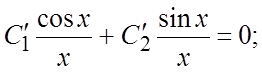 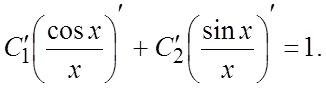 Отсюда найдем:  Интегрируя найденные два ДУ, получим   По  формуле  (6.8)  запишем

общее решение НЛДУ: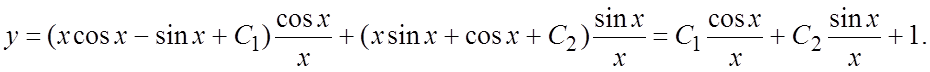

Пример 9. Проинтегрировать уравнение , зная что соответствующее ОЛДУ имеет частное решение .

Решение. 1. Найдем общее решение ОЛДУ  (см. решение примера 7). Найдем :

 

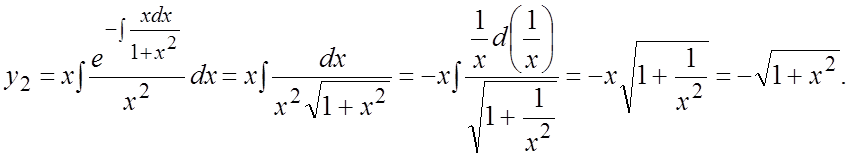
Общее решение ОЛДУ: 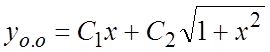. 2. Найдем общее решение НЛДУ. а) очевидно, что y =1 есть частное решение и по формуле (6.7) общее решение НЛДУ: 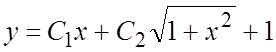. б) найдем общее решение по методу вариации произвольных постоянных. Составляем систему (6.9), приведя исходное уравнение к виду (6.1): 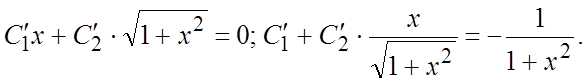  Решим систему алгебраически: 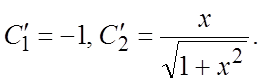 Интегрируя, найдем:   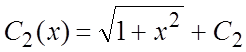и общее решение НЛДУ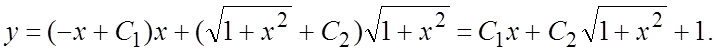  

10.6.2. Линейные уравнения  n- го порядка с постоянными 

коэффициентами

1)         Однородные линейные уравнения с постоянными

коэффициентами

Рассматриваем уравнение (6.2), считая в нем коэффициенты . Это уравнение имеет ФСР , определенную и состоящую из степенных, показательных и тригонометрических функций. Соответствующее ей общее решение  определено в области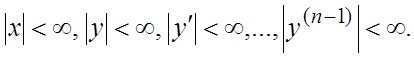

          ФСР ОЛДУ строится по методу Эйлера: частное решение ОЛДУ ищем в виде

                                                             ,                                                   (6.10)

где  - некоторое постоянное число (вещественное или комплексное), подлежащее определению. Для его определения составляют характеристическое уравнение

                                        .                              (6.11)

Структура ФСР зависит от вида корней  уравнения (6.11).

1. Все корни характеристического уравнения (6.11) различны и вещественны. ФСР в этом случае имеет вид  и общее решение запишется по формуле (6.3): .

2. Все корни (6.11) различны, но среди них имеются комплексные. Пусть - комплексный корень; тогда - тоже корень (6.11). Этим двум корням соответствуют два линейно независимых частных решения . Если корни  и  чисто мнимые: , то соответствующие линейно-независимые решения: . Корням  в формуле общего решения (6.3) соответствует выражение вида , а чисто мнимым корням  отвечает сумма .

3. Среди корней характеристического уравнения (6.11) имеются кратные корни.

а).Пусть - вещественный k- кратный корень. Тогда ему соответствует k линейно независимых частных решений , а в формуле (6.3) – выражение вида .

б). Если  есть комплексный корень (6.11) кратности k, то ему и сопряженному с ним корню той же кратности соответствуют 2k линейно независимых частных решений вида

                              

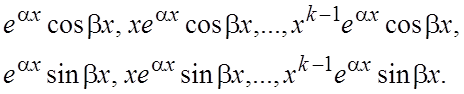
В формуле общего решения (6.3) этим корням соответствует выражение вида

.

Паре чисто мнимых корней  кратности k отвечает сумма

.

Пример 1. Найти общее решение уравнения .

Решение. Характеристическое уравнение (6.11) имеет вид , откуда - действительные различные числа. Общее решение (см. п.1): .

Пример 2. Проинтегрировать уравнение .

Решение. Уравнение (6.11):  имеет корни . Корни действительные, причем один из них: - двукратный. Общее решение имеет вид (см. п.3,а)): .

Пример 3. Найти общее решение уравнения .

Решение. Характеристическое уравнение  имеет корни . Следовательно (см. п.2), функции  составляют ФСР, а общее решение имеет вид: .

Пример 4. Найти частное решение уравнения , удовлетворяющее начальным условиям: .

Решение. Характеристическое уравнение  имеет единственный корень кратности k =3. ФСР имеет вид (п.3,а)): ; следовательно,  - общее решение.

          Для определения произвольных постоянных найдем производные:

.

Подставляя в  и начальные данные, получим систему: , , , откуда находим . Искомое частное решение: .

Пример 5. Найти общее решение уравнения .

Решение. Характеристическое уравнение  или  имеет корни - простой и - пара двукратных мнимых корней. Обще решение (см. п.3,б): .

Пример 6. Проинтегрировать уравнение .

Решение. Уравнение (6.11) имеет двукратные комплексные корни ,  и, следовательно, общее решение (см. п.3,б)): .