Всякое решение уравнения (6.1) является частным решением, так что особых решений оно не имеет.
Однородное линейное уравнение (ОЛДУ)
![]() (6.2)
(6.2)
(всегда) имеет
нулевое решение ![]() , удовлетворяющее нулевым
начальным условиям
, удовлетворяющее нулевым
начальным условиям ![]() при
при ![]() и оно
единственно.
и оно
единственно.
Теорема 2. Общее решение ОЛДУ есть линейная комбинация решений ![]() его фундаментальной системы:
его фундаментальной системы:
![]() .
(6.3)
.
(6.3)
Определение 2. Фундаментальной системой решений (ФСР) уравнения
(6.2) называется n его любых линейно-независимых
частных решений ![]() .
.
Замечание. Для любого ОЛДУ существует бесконечное число фундаментальных систем решений.
Определение 3. Система из n функций
![]() называется линейно-независимой ( на (a,b)) системой, если
тождество
называется линейно-независимой ( на (a,b)) системой, если
тождество
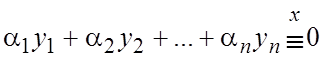 (6.4)
(6.4)
выполняется лишь
в случае ![]() .
.
Теорема 3. Чтобы система решений ![]() была
фундаментальной, необходимо и достаточно, чтобы ее определитель Вронского
была
фундаментальной, необходимо и достаточно, чтобы ее определитель Вронского
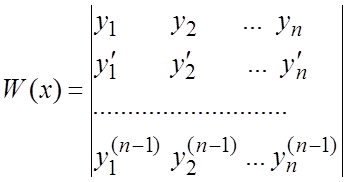 (6.5)
(6.5)
был отличен от
нуля хотя бы в одной точке интервала ![]() .
.
Ниже (§10.6.2) показывается, что построить ФСР в элементарных функциях удается всегда для уравнений с постоянными коэффициентами – для этих уравнений легко находится общее решение. Для уравнений с переменными коэффициентами общего (точного) метода построения ФСР не существует.
Пример 1. Показать, что система функций ![]() линейно
независима на интервале (
линейно
независима на интервале (![]() .
.
Решение. Равенство (6.4) может выполняться ![]() лишь
при условии, что
лишь
при условии, что ![]() ; иначе в левой части будем иметь
многочлен степени не выше третьей, который может обратиться в нуль не более,
чем при трех значениях x из данного интервала.
; иначе в левой части будем иметь
многочлен степени не выше третьей, который может обратиться в нуль не более,
чем при трех значениях x из данного интервала.
Пример 2. Показать, что система функций ![]() ,
где
,
где ![]() попарно различны, линейно независима на
интервале
попарно различны, линейно независима на
интервале ![]() .
.
Решение. Предположим противное; тогда в тождестве (6.4) ![]() . Пусть это
. Пусть это ![]() . Деля
обе части тождества (6.4) на
. Деля
обе части тождества (6.4) на ![]() , получим:
, получим: ![]() . Дифференцируя это тождество и деля обе
части его на
. Дифференцируя это тождество и деля обе
части его на ![]() , придем к тождеству
, придем к тождеству ![]() . Дифференцируя, получим
. Дифференцируя, получим ![]() , что невозможно, так как
, что невозможно, так как ![]() по предположению,
по предположению, ![]() по
условию, а
по
условию, а ![]() .
.
Замечание. Для случая двух функций критерием их линейной независимости является отношение их, тождественно не равное постоянной.
Пример 3. Функции tgx и ctgx линейно независимы в интервале ![]() , так как их отношение
, так как их отношение 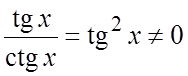 в этом интервале. Функции sin2x и
в этом интервале. Функции sin2x и ![]() линейно зависимы в интервале
линейно зависимы в интервале ![]() , так как их отношение
, так как их отношение 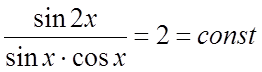 в этом интервале (в точках разрыва функции
в этом интервале (в точках разрыва функции
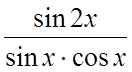 доопределяем это отношение по
непрерывности).
доопределяем это отношение по
непрерывности).
Пример 4. Найти определитель Вронского для функции ![]() .
.
Решение. Имеем
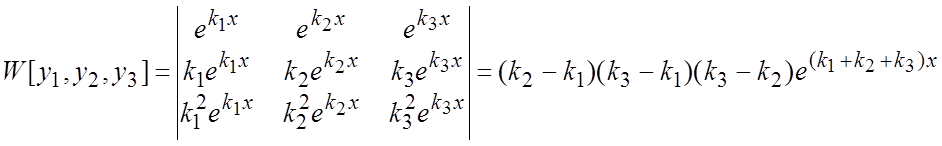 .
.
Пусть ![]() есть система из n
линейно-независимых на отрезке [a,b] функций, имеющих все производные до n-го порядка включительно. Тогда уравнение
есть система из n
линейно-независимых на отрезке [a,b] функций, имеющих все производные до n-го порядка включительно. Тогда уравнение
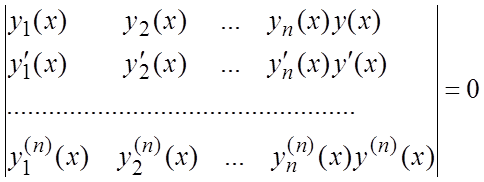 (6.6)
(6.6)
где ![]() - независимая функция, определяет ДУ, для
которого функции
- независимая функция, определяет ДУ, для
которого функции ![]() составляют ФСР.
составляют ФСР.
Пример 5. Составить ДУ, для которого функции 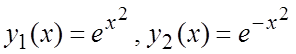 образуют ФСР.
образуют ФСР.
Решение. Составим уравнение (6.6):
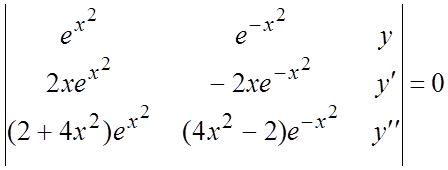 или
или 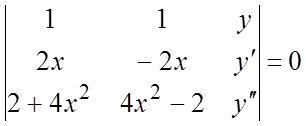 .
.
Раскрывая
последний определитель по элементам третьего столбца, получим искомое
уравнение: ![]() .
.
Замечание. В данном примере определитель Вронского ![]() обращается в ноль при
обращается в ноль при ![]() , что не противоречит общей теории, так как
записав уравнение в виде
, что не противоречит общей теории, так как
записав уравнение в виде 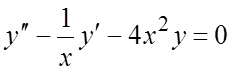 , обнаружим, что
коэффициент при
, обнаружим, что
коэффициент при ![]() терпит разрыв при
терпит разрыв при ![]() .
.
Если
известно какое-либо частное решение ![]() уравнения (6.2), то
подстановка
уравнения (6.2), то
подстановка ![]() приводит это уравнение к линейному
уравнению относительно функции
приводит это уравнение к линейному
уравнению относительно функции ![]() , не содержащему (явно)
этой функции и, следовательно, подстановка
, не содержащему (явно)
этой функции и, следовательно, подстановка ![]() понижает
порядок этого уравнения на единицу.
понижает
порядок этого уравнения на единицу.
Пример 6. Найти общее решение уравнения ![]() ,
если функция
,
если функция ![]() есть его частное решение.
есть его частное решение.
Решение. Подставив ![]() в уравнение,
убеждаемся в том, что
в уравнение,
убеждаемся в том, что ![]() , действительно, является его
частным решением. Положим
, действительно, является его
частным решением. Положим ![]() , найдем
, найдем ![]() . Подставив
. Подставив ![]() в
уравнение, после преобразования придем к уравнению
в
уравнение, после преобразования придем к уравнению ![]() .
Полагая здесь
.
Полагая здесь ![]() , придем к уравнению первого
порядка относительно функции
, придем к уравнению первого
порядка относительно функции ![]() , общее решение
которого имеет вид
, общее решение
которого имеет вид 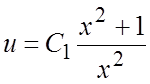 . Учитывая, что
. Учитывая, что ![]() , придем к уравнению
, придем к уравнению 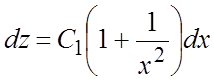 , интегрируя которое, найдем:
, интегрируя которое, найдем: 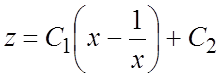 . Заменяя z
по формуле
. Заменяя z
по формуле ![]() , получим общее решение исходного
уравнения:
, получим общее решение исходного
уравнения: ![]() .
.
Замечание 1. Изложенный метод обобщается на случай, когда известны k частных линейно-независимых решений уравнения (6.2).
Замечание 2. Для построения общего решения ОЛДУ ![]() достаточно знать только одно ненулевое
частное решение его. При этом второе частное решение
достаточно знать только одно ненулевое
частное решение его. При этом второе частное решение ![]() можно
найти по формуле
можно
найти по формуле 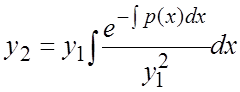 .
.
Пример 7. Найти общее решение уравнения ![]() ,
если оно имеет частное решение
,
если оно имеет частное решение ![]() .
.
Решение. Найдем 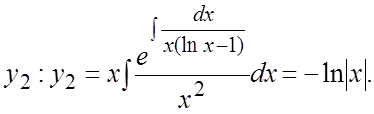 Поэтому общим
решением уравнения будет
Поэтому общим
решением уравнения будет ![]() .
.
2°. Неоднородные уравнения (НЛДУ). Приведем теорему о структуре общего решения НЛДУ.
Теорема 4. Общее решение НЛДУ (6.1) есть сумма общего решения
(6.3) ОЛДУ (6.2) и любого частного решения![]() НЛДУ
(6.1):
НЛДУ
(6.1):
![]() (6.7)
(6.7)
Все решения НЛДУ содержатся в формуле (6.7).
Пользование формулой (6.7) на практике затруднительно, так как метод определения частного решения НЛДУ получен лишь для уравнений с постоянными коэффициентами и с правой частью некоторого специального вида.
Приведем одно свойство решений НЛДУ (принцип суперпозиции решений): если правая часть НЛДУ (6.1) состоит из нескольких слагаемых и для НЛДУ с той же левой частью и правой частью, равной каждому из этих слагаемых в отдельности, мы можем найти частное решение, то сумма последних будет частным решением всего уравнения (6.1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.