Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 9

Течение (2.6) состоит из суммы двух движений. Первое – это простое течение Куэтта. Оно описывается первыми членами соотношений (2.6), (2.9), (2.10) и получается при нулевом градиенте давления  = 0, представляя собой чисто сдвиговое течение с линейным профилем скорости. Второе – это течение Пуазейля (вторые члены вышеперечисленных соотношений). Оно описывает течение между неподвижными плоскостями под действием сил давления при V = 0. В этом случае получается параболический профиль скорости с максимальным значением скорости посередине слоя.

Для общего случая течения (2.8) при  давление падает при увеличении координаты x. Профиль скорости будет наполненным (рис. 3). Для  течение будет более сложным. Оно определится конкуренцией сил вязкости, увлекающих жидкость в направлении движения плоскости, и сил давления, направленных в противоположную сторону. Для  появляется возвратное течение.

2.2.  Течение Куэтта между нагретыми плоскостями

Рассмотрим течение несжимаемой теплопроводной жидкости между двумя параллельными плоскостями, температура которых T₀ и T₁, скорости - 0 и V, расстояние между ними - h (рис.4). Течение будем считать стационарным, физические характеристики жидкости – постоянными. Так как жидкость несжимаема, уравнения движения можно решать независимо от уравнения энергии. Их решение было получено выше:

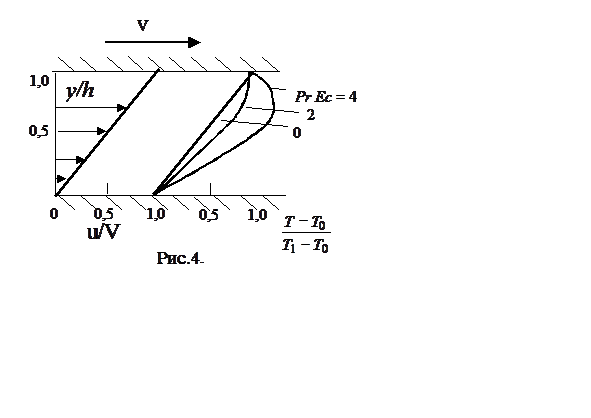
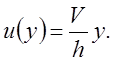               (2.11)

В уравнении энергии (1.33) все конвективные члены равны нулю. Останутся только члены, определяющие теплопроводность и выделение тепла за счет трения.

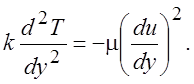   (2.12)

Граничные условия:

T = T₀  при  y = 0,

(2.13)

T = T₁  при  y = h.

Подставляя выражение (2.11) в (2.12), получим

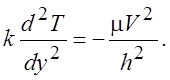                                                (2.14)

Общее решение (2.14) запишем в виде

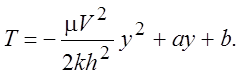                                      (2.15)

Из граничных условий находим

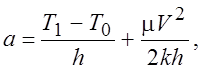  b = T₀.                              (2.16)

Решение задачи (2.14) с граничными условиями (2.13) можно представить в виде

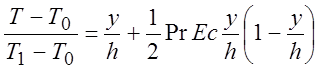,                                    (2.17)

где число Эккерта определено как . Решение (2.17) (см. рис. 4) напоминает решение (2.6) и также является суперпозицией линейного и параболического распределений.

Тепловой поток определяется производной от температуры по нормальной координате.

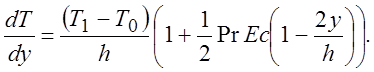                             (2.18)

Пусть T₁ – T₀ > 0 (движущаяся поверхность нагрета сильнее).

Тогда при y = h

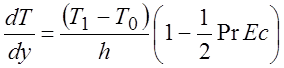.                                         (2.19)

При выполнении условия 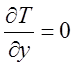 меняется направление теплопередачи. Оно соответствует теплоизолированной поверхности, т.е. тепло не передается стенке. Из (2.19) следует, что 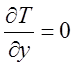 при выполнении условия Pr Ec = 2. Для случая Pr Ec > 2 тепло передается от жидкости к стенке (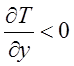); для Pr Ec < 2 от стенки к жидкости ().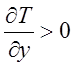

При движении вязкой жидкости за счет внутреннего трения происходит нагрев жидкости и стенок, с которыми она соприкасается. Пусть обе поверхности нагреты одинаково – T₁ = T₀. Тогда из (2.17) следует, что

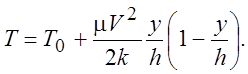                                     (2.20)

Максимальная температура достигается при y = 0,5 h

                                                (2.21)

Температура теплоизолированной поверхности Т_е определяется из условия . Она равна

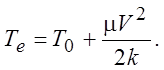                                          (2.22)

Запишем выражения для Т_max (2.21) и Т_е (2.22) через число Маха М и Прандтля Pr, с использованием скорости звука :

                              

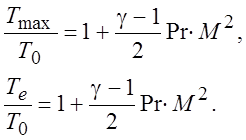
Видно, что нагрев жидкости зависит от скорости течения и пропорционален квадрату числа Маха.

2.3.  Течение Гагена – Пуазейля

Течением Гагена – Пуазейля называют установившееся осесимметричное течение в прямой трубе круглого сечения. Если использовать цилиндрические координаты (r, q, z) и обозначить через u составляющую скорости вдоль z, то  можно принять

                                                  

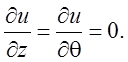
Тогда систему уравнений движения можно представить в виде

                                                    

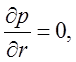
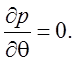
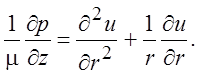                                            (2.23)