Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 11

3.1.  Обтекание шара. Приближение Стокса

В качестве примера ползущего движения рассмотрим прямолинейное и равномерное движение шара со скоростью V через вязкую жидкость (G.G.Stokes, 1851). Задача о движении шара эквивалентна задаче об обтекании неподвижного шара потоком, имеющим на бесконечности скорость V. Будем рассматривать течение в системе координат, начало которой совпадает с центром шара, ось ox направлена вдоль течения, расстояние до точки с координатами (x, y, z ) задается радиусом r² = x² + y² + z². Радиус шара равен r_o._. Для p выбирается выражение

                                                     (3.2)

Это есть так называемое разложение по мультиполям. Здесь использован член в виде диполя, так как задача имеет осевую симметрию и возмущения давления должны иметь выделенное направление вдоль оси х. Третья степень в выражении (3.2) связана с тем, что полная энергия возмущений давления в окружающем пространстве создаваемая шаром, при r ® ¥ должна быть конечной, так как объем растет » r³. Подстановка (3.2) в (3.1) дает:

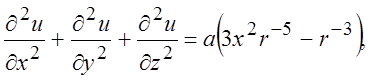
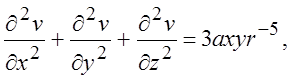                                         (3.3)

                                        

                                        

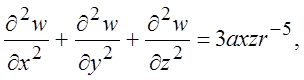
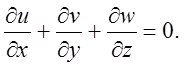
Граничные условия:

                                         u = v = w = 0   при  r = r₀,

u = V,  v = 0,  w = 0  при  r ® ¥                                       (3.4)

Общим решением системы (3.3) будут выражения

                              

                                  

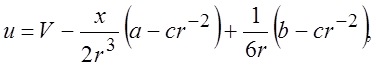
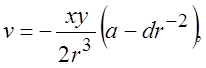
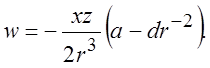
Граничные условия (3.4) на бесконечности удовлетворятся автоматически.

Уравнение неразрывности примет вид

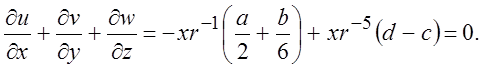                        (3.5)

Соотношение (3.5) должно выполняться для любого r, что дает два условия для определения констант:

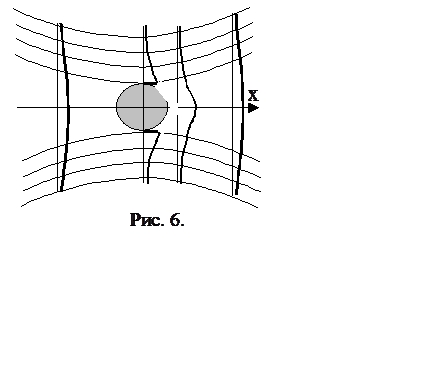
                  (3.6)

Еще два условия получим из граничных условий (3.4) на поверхности

                                (3.7)

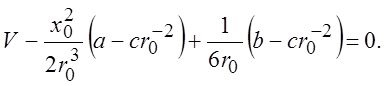
В результате решения системы (3.6) и (3.7) находим константы интегрирования

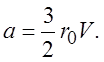                                      (3.8)

Тогда для давления и скоростей в потоке получаем следующие соотношения

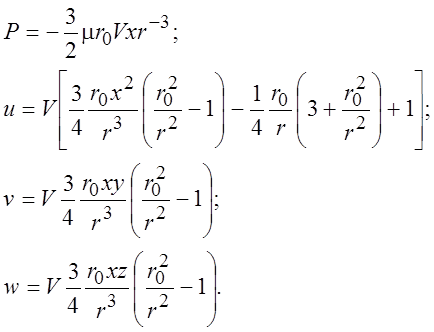          (3.9)

В дальнейшем, в силу симметрии задачи, скорость вдоль оси z рассматриваться не будет. Рассмотрим структуру течения вдали от шара. Тогда r₀/r << 1 и отношениями радиусов в круглых скобках можно пренебречь. Учитывая, что 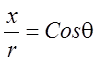 и 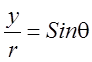, где q - угол отсчитываемый в плоскости (x,y) от направления –х, получаем

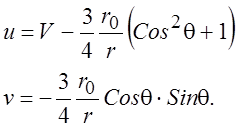                                                            (3.10)

Видно, что скорость u в (3.10) увеличивается от некоторого значения до угла 90° и затем снова до него падает. Скорость v вначале равна нулю, затем достигает максимума при угле 45° и при угле 90° снова падает до нуля. Для углов больших 90° картина повторяется в обратном порядке. В этих условиях, линии тока (касательные к суммарной скорости компонент) должны вести себя так, как показано на рис. 6. Симметрия картины течения следует и из уравнений (3.1). При обращении знака при скоростях и давлении уравнения переходя сами в себя.

Определим силу, действующую на шар. Она состоит из силы давления р и касательных напряжений t. Для этого получим профиль скорости вблизи поверхности шара, где r = r₀ + x, x << r₀. Разложим члены с отношением радиусов в (3.9) в ряд Тейлора до второго члена

       

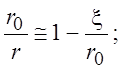
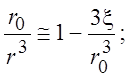
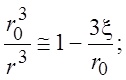
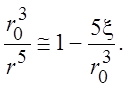
и подставим в (3.9) и после сокращений получим

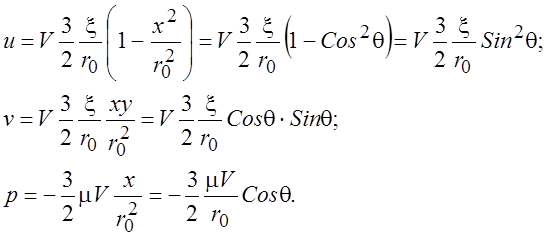                                             (3.11)

Сила поверхностного трения по определению

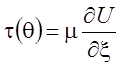                                         , где .

Отсюда

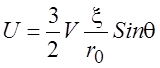 и 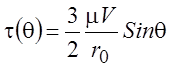          .                               (3.12)

Полную силу, действующую на шар, получим интегрированием по поверхности шара с учетом направляющих углов

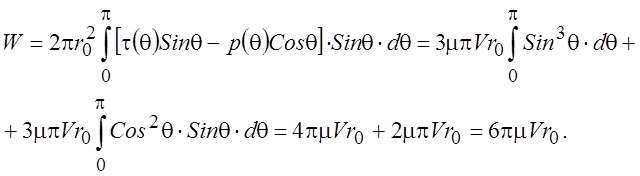                     (3.13)

Выражение (3.13) получило название формулы Стокса. Из (3.13) видно, что только треть всей силы сопротивления шара связаны с силами давления.

Найдем коэффициент сопротивления шара

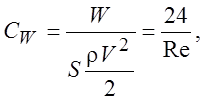                                                       (3.14)

здесь S - площадь сечения; Re = VD/v - число Рейнольдса, рассчитанное по диаметру шара D = 2r₀ .