При выводе уравнения энергии не обсуждались ограничения на величину числа Маха и величина q/Re была принята » d2 (см. уравнение (4.12)). Легко показать, что q » М2 и при умеренных числах Рейнольдса и достаточно больших числах Маха это условие нарушается.
Оценим порядок величины M2/Re. Введем еще один характерный размер – длину свободного пробега l. Для динамического коэффициента вязкости из курса физики знаем следующую оценку:
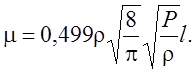 (4.25)
(4.25)
Из (4.25) получим выражение для длины свободного пробега
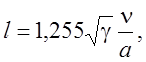
где ![]() - скорость звука. Для больших чисел
Рейнольдса можно составить следующее соотношение:
- скорость звука. Для больших чисел
Рейнольдса можно составить следующее соотношение:
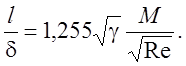 (4.26)
(4.26)
Отношение
длины свободного пробега к характерному размеру задачи называют числом Кнудсена
![]() . Оно характеризует степень разреженности
газа. Интересующая нас величина
. Оно характеризует степень разреженности
газа. Интересующая нас величина ![]() и она не должна быть
велика, т.е. уравнения пограничного слоя справедливы для не очень разреженных
газов.
и она не должна быть
велика, т.е. уравнения пограничного слоя справедливы для не очень разреженных
газов.
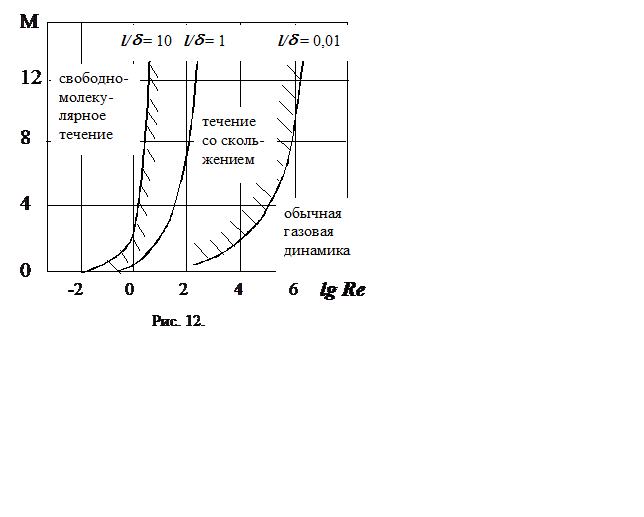 Пользуясь числом Кнудсена, можно весьма приближенно
наметить области применимости различных методов описания течения газов. На рис.
10 показана диаграмма (Tsien, 1946), разграничивающая
области в зависимости от чисел M, Re
и Kn.
Пользуясь числом Кнудсена, можно весьма приближенно
наметить области применимости различных методов описания течения газов. На рис.
10 показана диаграмма (Tsien, 1946), разграничивающая
области в зависимости от чисел M, Re
и Kn.
Переходная область от обычной газовой динамики к свободномолекулярному течению разделена на две подобласти. Введена подобласть течения со скольжением. В ней еще применимы уравнения пограничного слоя, но уже видоизменены граничные условия для температуры и скорости. Принимается предположение о наличии на поверхности обтекаемого тела скачков скорости и температуры.
Задача 4.1.
В случае равномерного отсоса пограничного слоя на пластине образуется ассимтотический профиль отсасывания, не зависящий от продольной координаты. Определить профиль скорости, интегральные толщины пограничного слоя и напряжение трения.
Задача 4.2.
Определить наименьший темп роста давления, при котором может произойти отрыв потока.
5. АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ УРАВНЕНИЙ
ПОГРАНИЧНОГО СЛОЯ
Автомодельными (подобными) решениями будем называть такие решения, для которых продольные составляющие скорости в двух различных поперечных сечениях отличаются друг от друга только масштабом координат. В этом случае уравнения пограничного слоя могут быть сведены к обыкновенным дифференциальным уравнениям.
5.1. Решения Фокнера-Скэн
Рассмотрим стационарное течение несжимаемой жидкости в пограничном слое, когда
![]() (5.1)
(5.1)
где с и m - постоянные, причем m - безразмерная. Выражение (5.1) описывает симметричный потенциальный поток, омывающий клин с углом при вершине pb, где b = 2m/(m+1). Если m > 0, то поток ускоряется и вершина клина x = 0 является точкой торможения. Для m = 0 получаем равномерный поток, омывающий полубесконечную плоскую пластину. В случае замедляющегося потока с m < 0 окрестность точки x = 0 должна быть исключена из рассмотрения.
Задача описывается системой уравнений
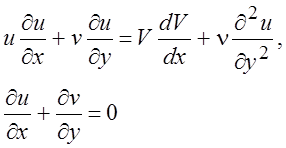 (5.2)
(5.2)
с граничными условиями
u(0) = v(0) = 0, u(¥) = V. (5.3)
Введем функцию тока такую, что
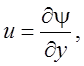
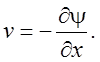 (5.4)
(5.4)
При выполнении соотношений (5.4) уравнение неразрывности в системе (5.2) выполняется автоматически. Уравнение движения можно записать в виде
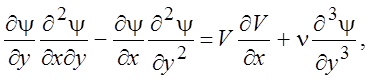 (5.5)
(5.5)
с граничными условиями
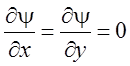 при y = 0, (5.6)
при y = 0, (5.6)
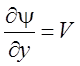 при y =
¥.
при y =
¥.
Подставим (5.1) в уравнение (5.5) и сделаем замену переменных
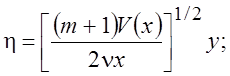
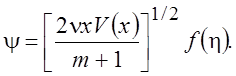 (5.7)
(5.7)
Получаем уравнение Фокнера-Скэн (Folkner, Skann, 1931):
![]() (5.8)
(5.8)
с граничными условиями
![]()
![]() (5.9)
(5.9)
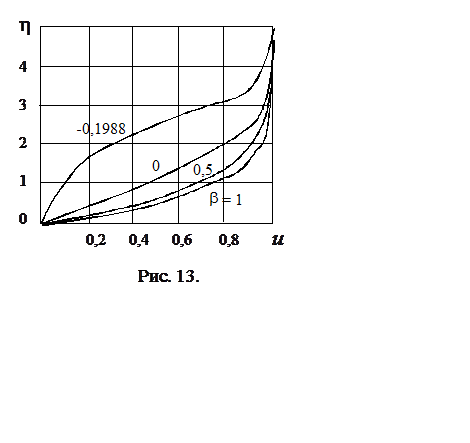 Распределение скорости дается выражением
Распределение скорости дается выражением ![]() ,
, 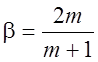 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.