Вычисление погрешности функций. Определение допустимой погрешности аргументов по допустимой погрешности функций

             б) 0,096835;   .                               б) 0,66385; .

        3) а)12,688 ;  б) 4,636.                                    3)   а) 6,743;   б) 0,543 .

18.4. ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ФУНКЦИЙ

18.4.1. Функции одной переменной. Абсолютная погрешность дифференцируемой функции , вызываемая достаточно малой погрешностью аргумента , оценивается величиной

                                                              ,                                          (18.12)

          Если значения функции  положительны, то для относительной погрешности имеет место оценка

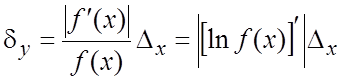                                                  .                             (18.13)

          Например, для тригонометрических функций абсолютные погрешности синуса и косинуса не превосходят абсолютных погрешностей аргумента:

                                          ,    .         (18.14)

18.4.2. Функции нескольких переменных.   Пусть задана некоторая функция , от п аргументов  и пусть значения каждого из аргумен­тов , определены с некоторыми погрешностями , i = 1, 2,..., п. Требуется найти погрешность данной функции.

Для решения этой задачи будем предполагать, что функция  является дифференцируемой в некоторой области D. Абсолютная погрешность  функции y при заданных абсолютных погрешностях  аргументов  равна

                      .             (18.15)

Предполагая, что величины , i = 1, 2,..., п  достаточно малы, можно записать приближенные равенства

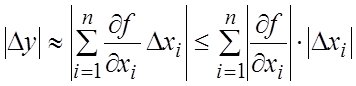                                                                              (18.16)

Следовательно, предельная абсолютная погрешность  функции y равна

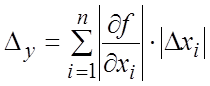                                                    ,                                              (18.17)

где  предельная абсолютная погрешность аргумента .

Оценка для относительной погрешности функции получается путем деления обеих частей неравенства (18.15) на

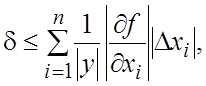                                                                                       (18.18)

Из формулы (18.18) получаем выражение для предельной отно­сительной погрешности функции у

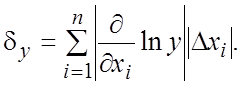                                                                                             (18.19)

Рассмотрим отдельные примеры на вычисление погрешностей различных функциональных соотношений. Будем предполагать, что в каждом примере заданы те или иные погрешности аргументов.

1. Пусть . По формуле (18.17) предель­ная абсолютная погрешность суммы п слагаемых равна

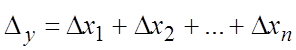                                          .                             (18.20)

2. Пусть . По формуле (18.17) предельная абсолют­ная погрешность разности двух чисел равна

.

3. Пусть  , причем x_i  (i=1, 2, ..., п) положительны. В соответствии с формулой (18.19) проведем  преобразования с целью получения выражения для предельной относительной погрешности произведения п сомножителей

.

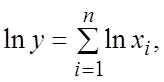
4. Пусть 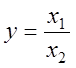. По формуле (18.19) предельная относительная погрешность частного равна  

                                                .

5. Пусть . Тогда .

.

6. Пусть . Следовательно, .

.

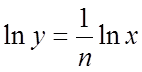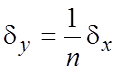18.5.    Определение допустимой погрешности аргументов по допустимой погрешности функций

Задача определения какими должны быть погрешности исходных приближений, чтобы полученный результат имел заданную степень точности, имеет однозначное решение только для функции одной переменной : если  эта функция дифференцируема и  , то

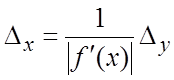                                                      .                                               (18.21)

          Для функций нескольких переменных  эта задача решается неоднозначно. Для ее решения необходимо наложить какие-либо условия на погрешность исходных данных. Если использовать принцип равных влияний, считая что в формуле (18.17) все слагаемые 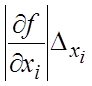 равны между собой, получим

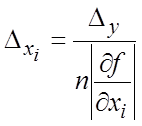
                                                .                                             (18.22)

Пример 8. Даны числа ; . Тогда . Причем последняя цифра сомнительная.

Пример 9. Найти сумму , где ; ; . Причем все цифры верные.

  Имеем . Предельная абсолютная погрешность суммы . Стало быть, 7.84 < y< 7.87. В результате верными будут цифры 7.8. Последняя цифра 4 сомнительная. #