Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 7

(24018*vo+48307)/98000

v1:=vo+0.3*vo1+vo2*(0.3)^2/2+vo3*(0.3)^3/6

(2099500*vo-129339)/3430000

2*u1+3*v1=1.2

SOLVE(2*u1+3*v1=1.2,vo);

Simp(#9)

[vo=1122527/7979760]; Approx(#10)

[vo=5122/36411=0.140671]

тоді розв’яжемо систему:

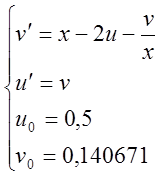
//x0 – початкове значення

//xn – кінцеве значення

//h – початковий крок

//X,Y – масиви результатів

Prognose_Correction(x0,u0,v0,h,X,Y):

1  u01:=v01;

2  v01:=x0-2*u0-v0/x0

3  u02:=v01

4  v02:=1-2*u01-((v01*x0-v0)/sqr(x0))

5  u03:=v02

6  v03:=-2*u02-((v02*x0*sqr(x0)-2*v01*sqr(x0)+2*v0*x0)/sqr(sqr(x0)))

7  u1:=u0+h*u01+h*h*u02/2+h*h*h*u03/6

8  v1:=v0+h*v01+h*h*v02/2+h*h*h*v03/6

9  i:=0

10  while (x1<=xN) do

11   i++

12   repeat

13   x1:=x0+i*h

14   x2:=x0+(i+1)*h

15   v11:=x1-2*u1-v1/x1

16   u11:=v1

17   p2:=u0+2*h*u11

18   p2z:=v0+2*h*v11

19   u2:=p2

20   v2:=p2z

21   u21:=p2z

22   v21:=x2-2*p2-p2z/x2

23   c2z:=v1+h*(v11+v21)/2

24   v2:=c2z+(p2z-c2z)/5

25   u21:=v2

26   c2:=u1+h*(u11+u21)/2

27   u2:=c2+(p2-c2)/5

28   if abs(p2-c2)<eps then

29   X[i]:=x2;

30   Y[i]:=u2;

31   fi

32   if abs(p2-c2)>e then

33   h:=h/2;

34   fi

35   until abs(p2-c2)<eps;

36  done//while

end

8.2.2 Методи Адамса

На відміну від однокрокових методів, у яких числовий розв’язок одержують тільки з диференціального рівняння і початкової умови, алгоритми Адамса складаються з двох частин: перша з них – стартова процедура для визначення  (наближені значення точного розв’язку в точках ), а друга – багатокрокова формула для одержання наближеного значення точного розв’язку . Потім ця формула застосовується рекурсивно для того, щоб за числовим розв’язком на  послідовних кроках обчислити  і т.д.

Стартові значення можна одержати декількома способами. Дж. К. Адамс обчислював їх за допомогою розкладання точного розв’язку в ряд Тейлора. Інший спосіб полягає у використанні якого-небудь однокрокового методу, наприклад, Рунге-Кутта. Стартові значення часто також обчислюють методами Адамса низького порядку з дуже малим кроком.

Розглянемо чисельні методи розв’язання задачі Коші (8.1)-(8.2), які  можуть бути задані формулою

.       (8.25)

Тут значення розв’язку  в точці  визначається через значення розв’язку в  точках, що передують . Такий метод називається  - кроковим.

З класу (8.25) виділимо багатокрокові методи вигляду

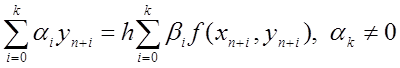,           (8.26)

застосовувані на сітці з постійним кроком

     (8.27)

Різниця між найбільшим і найменшим значеннями індексу невідомої функції у_n, що входить у рівняння (8.26), дорівнює . Тому співвідношення (8.26) є різницевим рівнянням -го порядку, загальний розв’язок якого залежить від  параметрів. Щоб виділити єдиний розв’язок цього рівняння, необхідно задати  додаткових умов на функцію у_п. Цими додатковими умовами є значення функції у_n при n = 0,1,... , -1:

                 (8.28)

які передбачаються відомими.

Використовуючи значення (8.28), з рівняння (8.26) при n=0 можна знайти , потім, використовуючи значення  і покладаючи в (8.26) n =1, знайти  і т.д. Таким чином, даний метод чисельного розв’язання диференціального рівняння полягає в розв’язанні різницевої задачі Коші для різницевого рівняння (8.26) і початкових умов (8.28).

Якщо шуканий розв’язок  входить до правої частини цього рівняння, що буває, коли , то формула (8.26) визначає неявний метод. Якщо , то шуканий розв’язок до правої частини не входить і рівняння (8.26) може бути розв’язане відносно . У цьому випадку формула (8.26) визначає явний метод.