Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 10

Різницеве рівняння (8.45) має другий порядок точності, а (8.46) - третій. Щоб знайти область стійкості методу, варто записати аналогічні рівняння для диференціального рівняння (8.46). Наприклад, (8.45) набере вигляду

                           .

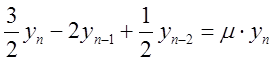Відповідне характеристичне рівняння запишеться в такий спосіб:

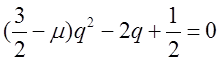                       .                         (8.47)

Потрібно визначити область комплексної площини , у точках якої обидва корені (8.47) за модулем менше одиниці. Виявляється, що ця область цілком розміщується у правій півплощині і метод (8.45) є  стійким.

8.3 Метод скінченних різниць

Основний зміст методу можна легко пояснити на прикладі розв'язання задач в одновимірній області.

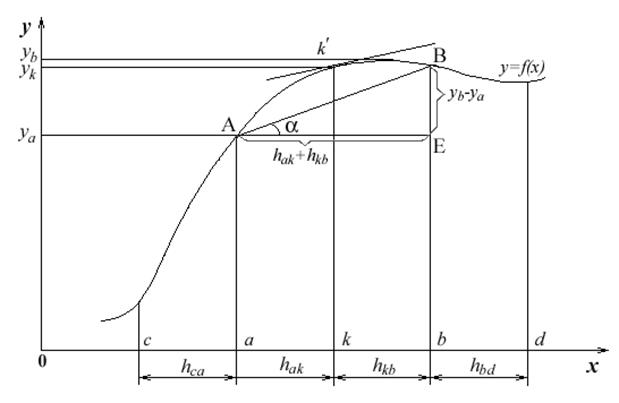
Рис. – 8.3

Виразимо похідну функції  лінійною комбінацією значень цієї функції у визначених точках розглянутого проміжку зміни незалежних змінних, які називаємо вузлами. Існує кілька способів вираження похідної подібним чином. Наприклад, першу похідну функції  у вузлі  (рис. 8.3) можна виразити такими скінченними різницями (дивись розділ 6):

(8.48)             (8.49) (8.50)

Відстань (крок) між вузлами беруть однаковою  і формула (8.50) записується у вигляді

(8.51)

Другу похідну можна наближено виразити (мал. 8.3), застосовуючи формулу (8.51) при  в такий спосіб:

(8.52)

Застосовується також формула для другої похідної, отримана на основі виразів (8.48), (8.49) для однобічних різниць (при ):

(8.53)

Розв'язання крайової задачі методом скінченних різниць зводиться до обчислення значень шуканої функції в обраних вузлах шляхом розв'язання відповідної системи лінійних алгебраїчних рівнянь.

Докладно розглянемо різницевий метод на прикладі крайової задачі для лінійного рівняння другого порядку з крайовими умовами першого роду

,                    (8.54)

 , .                        (8.55)

Уведемо на [a,b] сітку , що для спрощення викладень будемо вважати рівномірною. Наближено виразимо другу похідну від розв’язку через значення розв’язку у вузлах сітки ; наприклад, скористаємося найпростішою апроксимацією

.

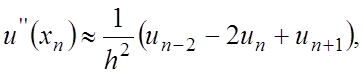
Таку апроксимацію можна записати в будь-якому вузлі сітки . Якщо підставити її в рівняння (8.54), то рівняння стане наближеним; точно задовольняти це рівняння буде вже не шуканий розв’язок , а деякий наближений розв’язок . Виконуючи цю підстановку і позначаючи  і , одержимо

  . (8.56)

Ця формула складається з N-1 алгебраїчного рівняння, а невідомими в ній є наближені значення розв’язку у вузлах сітки. Число невідомих  дорівнює N+1, тобто воно більше, ніж число рівнянь (8.56). Відсутні два рівняння легко одержати з крайових умов (8.55):

                             (8.57)

У випадку використання граничних умов другого роду апроксимація проводиться за допомогою формул чисельного диференціювання першого порядку:

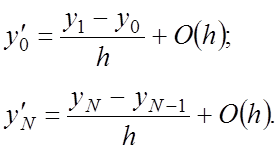
Розв’язуючи алгебраїчну систему (8.56), (8.57), знайдемо наближений розв’язок.

Як ілюстрацію проведемо повне дослідження розглянутого вище прикладу, додатково вимагаючи .

Спочатку розглянемо питання про існування різницевого розв’язку. Вихідна задача (8.54) була лінійною, різницева апроксимація (8.56)– теж лінійна. Завдяки цьому система (8.56,8.57) виявилася системою лінійних алгебраїчних рівнянь. Оскільки , то в матриці цієї системи діагональні елементи переважають: у кожному рядку модуль діагонального елемента більше суми модулів інших елементів, при цьому розв’язок лінійної системи існує і єдиний.

Обчислити розв’язок лінійної системи рівнянь завжди можна методом виключення Гауса. У даному випадку завдяки використанню триточкової апроксимації (8.54) система (8.56) має тридіагональну матрицю. Тому розв’язок доцільніше знаходити за допомогою різновиду методу Гауса – методом прогонки.