Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 11

Щоб оцінити похибку наближеного розв’язку задачі, використовують інформацію, отриману в процесі чисельних розрахунків (такі оцінки називаються апостеріорними). Найефективнішими можна вважати оцінки з подвійним перерахунком.

Наявність наближених значень  і , обчислених відповідно з кроками h і h/2, дає можливість зробити оцінку. Похибка методу – це , визначена в точці .

Отже, якщо , де М – невідомий коефіцієнт пропорційності, s – порядок точності методу, то

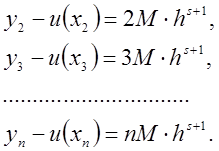
Виходить, для похибки в точці  при визначенні розв’язку з кроком h маємо рівність , а при розв’язку з кроком h/2 – рівність

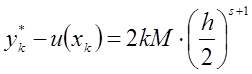.                  (8.58)

Знайшовши різницю між наведеними вище рівностями і розв’язавши отриману рівність відносно невідомого коефіцієнта М, визначимо

.

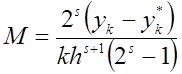Підставивши це значення М у формулу (8.58), одержимо 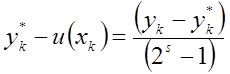. Звідси для абсолютної похибки в точці  остаточно одержимо таку рівність:

.

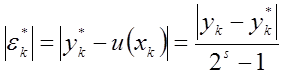Таку оцінку абсолютної похибки методу називають, як відомо,  правилом Рунге.

Зупинимося на стійкості розрахунку. Якщо , то задача Коші для рівняння (8.54) погано обумовлена, причому, чим більше p(x), тим гірша її стійкість. А з оцінки (8.58) видно, що похибка нашого різницевого розв’язку при великих p(x) мала. Звідси виходить, що добре побудовані різницеві схеми не чуттєві до нестійкості задачі Коші. У випадку, коли , не виконується достатня умова збіжності ітераційного процесу для систем лінійних алгебраїчних рівнянь, однак у практичних обчисленнях дана обставина, як правило, виявляється несуттєвою і не викликає складностей в одержанні розв’язку.

8.4 Різницева задача на власні значення

Розглянемо диференціальну задачу Штурма-Ліувілля

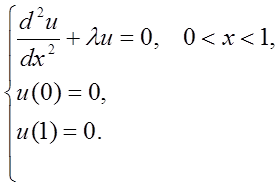
Числа  і відповідні функції u(x)0, що задовольняють поставлену крайову задачу називаються власними числами і власними функціями відповідно. Для даної задачі

Зауважимо, що функції u_m(x) є лінійно незалежними і взаємно ортогональними й можуть бути нормовані.

Для різницевої задачі на власні значення

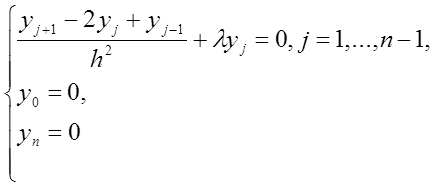
відповідні власні функції і власні значення різницевої задачі мають вигляд

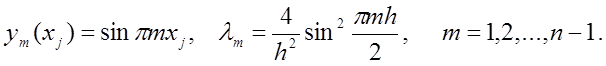
Відмітимо, що функції y_m(x) є лінійно незалежними і взаємно ортогональними, як і в диференціальному випадку, й можуть бути нормовані.

Питання і завдання до розділу 8

1  Постановка задачі Коші. Дискретна задача Коші: основні поняття і визначення  (сітка, сіткові функції, чисельний метод,  апроксимація, збіжність).

2  Виведення формули методу Ейлера, його геометрична інтерпретація,  стійкість, оцінка похибки, вплив обчислювальної похибки.

3  Методи Рунге-Кутта. Виведення формул. Оцінка похибки.

4  Явні однокрокові методи. Оцінка похибки за правилом Рунге.

5  Чисельне розв’язання задачі Коші для систем диференціальних рівнянь.

6  Апроксимація, стійкість  і збіжність  чисельних методів розв’язання задачі Коші.

7  Багатокрокові методи Адамса.

8  Виведення формул методу прогнозу і корекції.

9  Жорсткі задачі і методи їхнього розв’язання.

10  Застосовуючи метод Ейлера , знайти розв’язок задачі Коші 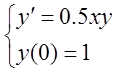 у трьох послідовних точках:

11  Для задачі Коші 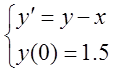 виконати один крок довжини 0.1 за методом Ейлера й оцінити похибку знайденого значення за правилом Рунге.

12  Методом Рунге-Кутта 2 порядку точності знайти розв’язок системи диференціальних рівнянь 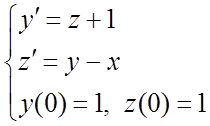 у двох послідовних точках ,.

13  Оцінити похибку апроксимації похідної різницевим відношенням .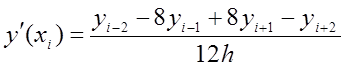

14  Звести рівняння другого порядку до системи рівнянь першого порядку і скласти розрахункові формули методу прогнозу і корекції для розв’язку отриманої системи рівнянь  , .

15  З'ясувати, чи апроксимують методи
a) 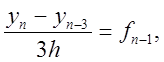 b)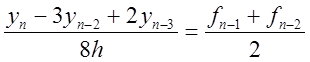
перше рівняння задачі Коші
 

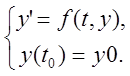
16  Для розв’язання задачі Коші 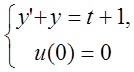 застосовується метод вигляду 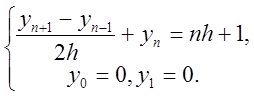 Визначити порядок апроксимації.

17  Дано систему ОДУ першого порядку з постійними коефіцієнтами , причому відомі власні значення матриці :
 a) ,
b) ,
c) .
У яких випадках систему можна вважати жорсткою?