Система. Еквівалентні математичні моделі. Рівняння регресії. Специфікація входів і виходів системи, страница 6

За заданим спектром – коренями квадратного рівняння – відтворимо заданий характеристичний поліном.

.

Його коефіцієнти  

Закон керування системою шукаємо у вигляді . При цьому невідому матрицю знаходимо за формулою . Матриця R є матрицею ,що дозволяє отримати еквівалентну заданій модель з простором станів, у якої подібною до матриці А буде її матриця Фробеніуса. Отже,

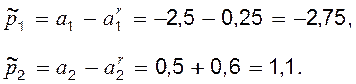
Для побудови матриці переходу  використаємо систему похідних

поліномів матриці А другого порядку:

.

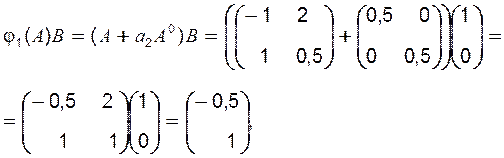
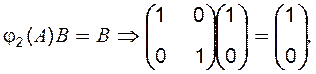
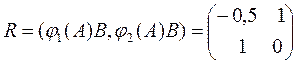Щоб уникнути обчислення оберненої матриці , невідому матрицю Р знайдемо з рівняння . Ця рівність для нашої задачі має такий вигляд:

.

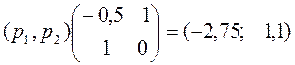Розв’язуємо систему

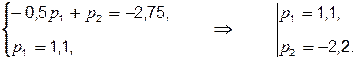
Отже, математичний закон керування  побудовано.

Модальне оцінювання станів. Для того щоб отриманий вище закон керування  міг використовуватися в реальних процесах керування, необхідно для поточного  знати  - стан системи. Однак стан – це спосіб вираження (чи представлення) закону, що формує динаміку системи, тобто він не є фізичним об'єктом і в принципі не може вимірюватися. Тому виникає задача одержання оцінок  координат вектора стану  для того, щоб ці оцінки  використовувати при виробленні керування.

Систему, у якій відбувається оцінювання станів, тобто її продуктом, чи, інакше, виходом є оцінка стану, будемо називати естиматором.

Отже, нехай задана  система, повністю спостережувана за виходом:

,              (6.22)

.                        (6.23)

Розглянемо задачу рекурентного оцінювання, вважаючи, що в кожен момент  відомі  й оцінка  стану. Будемо шукати оцінку , саме таку, щоб при  виконувалося . Це означає, що треба побудувати такий оператор , за допомогою якого знаходиться оцінка стану в момент  як  .

Система (6.22),(6.23) – лінійна, тому оператор  можна шукати в класі лінійних операторів, а саме

 .        (6.24)

Потрібно знайти такі матриці і , щоб  при .

Знайдемо рівняння, що описує поведінку .  Віднімемо обидві частини рівності (6.24) з (6.22):

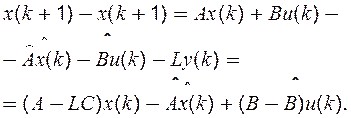     (6.25)

Щоб виконувалося , необхідно, насамперед, щоб права частина рівняння (6.25) не залежала від  . Тому одержуємо, що  повинно вибиратися як

 .                                    (6.26)

Якщо припустити  , то (6.25) набуде вигляду

 .      (6.27)

Таким чином, для забезпечення властивості  при  необхідно і достатньо, щоб система (6.27) була асимптотично стійкою. Отже, матриця  повинна бути обраною так, щоб усі власні числа матриці  були за модулем менші одиниці.

Розглянемо питання, коли ця задача має Розв’язання. Для цього покажемо, що власні числа матриць  і  (транспонованої) збігаються. Оскільки , то

.

З рівності характеристичних поліномів матриць  і  випливає рівність їхніх спектрів.

Отже, щоб існувала така матриця , щоб спектр матриці  збігався з будь-яким заздалегідь заданим спектром  , необхідно і достатньо, щоб ця задача мала розв'язок для матриці  , тобто для матриці  . А це буде справедливо, якщо пара  є повністю досяжною, тобто виконана умова

 .        (6.28)

Оскільки ранги будь-якої матриці і її транспозиції збігаються, то умова (6.28) еквівалентна умові  .

Таким чином, для того щоб задача синтезу системи оцінювання станів (6.24) могла бути розв’язаною, досить, щоб ця система була цілком спостережуваною.

Перейдемо до розгляду методу синтезу модальної системи оцінювання станів. Будемо вважати, що вихід  є скаляром, тобто матриця  є n-рядком. На підставі викладеного вище задача зводиться до визначення такого лінійного закону керування  для системи , що матриця  має заданий спектр . Дійсно, для  і  маємо . Згідно з (6.15) розв’язком цієї задачі є

 ,             (6.29)

де  .

Транспонуючи обидві частини рівності (6.29), знаходимо, що  є розв’язком системи алгебраїчних рівнянь  .

Розглянемо матрицю  .

Оскільки  для будь-якого і  , то 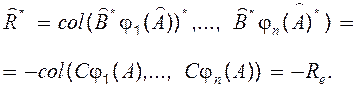 Остаточно одержуємо, що матрицю  можна знайти як розв’язок рівняння                 .                             (6.30)