Специфікація входів і виходів системи
Розглянемо систему, закон еволюції якої описується рівняннями
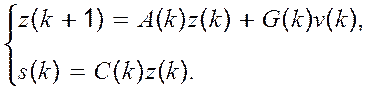 ( 6.1)
( 6.1)
Вхід v(k) може бути поділений на дві складові ![]() ) і
) і ![]() , тобто
, тобто ![]() , де складова
, де складова ![]() може
формуватися людиною, що впливає на систему (оператор, директор фірми і т.д.), а
складова
може
формуватися людиною, що впливає на систему (оператор, директор фірми і т.д.), а
складова ![]() є впливом навколишнього середовища на цю
систему і змінювати її значення неможливо. Значення
є впливом навколишнього середовища на цю
систему і змінювати її значення неможливо. Значення![]() формуються
об'єктивно іншими системами.
формуються
об'єктивно іншими системами.
Вхід ![]() називається керуванням,
а
називається керуванням,
а ![]() - збуренням.
- збуренням.
Тоді закон поведінки системи (6.1) може бути представлений як
![]() , (6.2)
, (6.2)
![]() . (6.3)
. (6.3)
Така система
призначена для виконання певних функцій, тобто вона перетворить за визначеним
законом сигнали, що надходять від інших систем. Розглянемо задачу
розроблення алгоритму керування системою. Є процес ![]() , що
може формуватися як у самій системі, так і надходити від іншої системи, і
треба, щоб у системі (6.2), (6.3) реалізовувався такий процес
, що
може формуватися як у самій системі, так і надходити від іншої системи, і
треба, щоб у системі (6.2), (6.3) реалізовувався такий процес ![]() , що
, що ![]() при
при
![]() , де
, де ![]() -
перша координата вектора
-
перша координата вектора ![]() (шляхом перестановки
рядків рівняння (6.3) завжди можна задачу звести до такої постановки).
(шляхом перестановки
рядків рівняння (6.3) завжди можна задачу звести до такої постановки).
Процес ![]() називається
сигналом, що задається, або впливом, що задається, чи просто
завданням. Оскільки він впливає на вихід системи, його можна розглядати як
вхід системи (6.2), (6.3).
називається
сигналом, що задається, або впливом, що задається, чи просто
завданням. Оскільки він впливає на вихід системи, його можна розглядати як
вхід системи (6.2), (6.3).
Отже, вхід розглянутої системи містить три специфічних процеси: керування, збурення і завдання.
Система, яка виробляє такі ![]() , що
виконується
, що
виконується ![]() при
при ![]() ,
називається слідкуючою.
,
називається слідкуючою.
Нехай ![]() - перший рядок матриці
- перший рядок матриці ![]() . Тоді можемо записати
. Тоді можемо записати ![]() .
.
Вище була виділена компонента ![]() вектора-виходу,
що мала особливе функціональне, стосовно поведінки системи, призначення. До
поводження інших компонентів поки що ніяких вимог не накладалося.
вектора-виходу,
що мала особливе функціональне, стосовно поведінки системи, призначення. До
поводження інших компонентів поки що ніяких вимог не накладалося.
Компоненту ![]() виходу s(k)
називають функціональною, а векторну компоненту
виходу s(k)
називають функціональною, а векторну компоненту ![]() –
інформаційною. В останній міститься інформація про стан
–
інформаційною. В останній міститься інформація про стан ![]() системи.
Вихід може бути поданий у вигляді
системи.
Вихід може бути поданий у вигляді ![]() ).
).
Задача синтезу органу керуванняполягає в
розробленні алгоритму для вироблення значень ![]() ) у
кожен момент за вимірами
) у
кожен момент за вимірами ![]() і
і ![]() для
для ![]() , що
забезпечує внаслідок рівнянь (6.2), (6.3) виконання умови
, що
забезпечує внаслідок рівнянь (6.2), (6.3) виконання умови ![]() при
при ![]() . При
цьому на процес
. При
цьому на процес ![]() можуть накладатися
додаткові вимоги. Наприклад, вимога, щоб при мінімальному
можуть накладатися
додаткові вимоги. Наприклад, вимога, щоб при мінімальному ![]() виконувалося
виконувалося ![]() для
усіх
для
усіх ![]() .
.
Синтез модального закону керування. Власні числа і власні вектори оператора або матриці в додатках часто називають модами. Набір власних чисел також називають спектром матриці.
Задача модального керування полягає в побудові такої
матриці ![]() , щоб власні числа матриці
, щоб власні числа матриці ![]() збігалися з заданим спектром
збігалися з заданим спектром ![]() . Якщо така матриця
. Якщо така матриця ![]() знайдена,
то поведінка системи
знайдена,
то поведінка системи
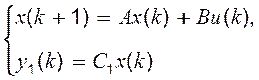 (6.14)
(6.14)
при
використанні закону керування ![]() буде визначатися
модами
буде визначатися
модами ![]() . Якщо при цьому
. Якщо при цьому ![]() ,
то система
,
то система
![]()
буде
асимптотично стійкою, тобто буде виконуватися ![]() при
при ![]() для будь-якого початкового стану
для будь-якого початкового стану ![]() .
.
Процедуру побудови матриці ![]() розглянемо
на випадок скалярного керування
розглянемо
на випадок скалярного керування ![]() . Матриця
. Матриця ![]() тоді є рядком
тоді є рядком ![]() ,
, ![]() вектором–стовпцем. Будемо вважати систему керованою,
тобто
вектором–стовпцем. Будемо вважати систему керованою,
тобто ![]() . У такому випадку вектори
. У такому випадку вектори ![]() лінійно-незалежні.
лінійно-незалежні.
Позначимо рядок ![]() , де
, де ![]() коефіцієнти полінома
коефіцієнти полінома ![]() . Розглянемо спектр
. Розглянемо спектр ![]() такий,
що
такий,
що ![]() . Вони можуть бути як дійсними, так і
комплексними. У полінома
. Вони можуть бути як дійсними, так і
комплексними. У полінома ![]() всі коефіцієнти
всі коефіцієнти ![]() є дійсними числами.
є дійсними числами.
Знайдемо таку матрицю ![]() , для
якої б виконувалась умова
, для
якої б виконувалась умова ![]() .
.
Розглянемо матрицю ![]() . Маємо
. Маємо
![]() і
і ![]() .
.
Нехай ![]() .
.
Оскільки 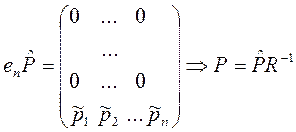 , то
, то
![]() .
.
Для виконання ![]() ,
необхідно прирівняти коефіцієнти при однакових степенях
,
необхідно прирівняти коефіцієнти при однакових степенях ![]() .
В результаті отримуємо
.
В результаті отримуємо ![]() , або
, або
![]() , тобто
, тобто
![]() .
(6.15)
.
(6.15)
Розв‘язок задачі модального керування задається формулою (6.15).
Приклад. Досліджувана система представлена моделлю з простором станів
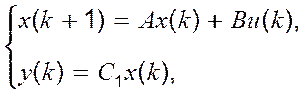 , де
, де 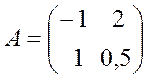 ,
,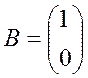 .
.
Необхідно
побудувати керування за заданим спектром ![]()
Розв’язання.
Характеристичний поліном матриці А другого порядку в загальному вигляді є таким:
![]() .
.
Знайдемо його за правилом обчислення визначника
![]() .
.
Отже, коефіцієнти характеристичного полінома ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.