Система. Еквівалентні математичні моделі. Рівняння регресії. Специфікація входів і виходів системи, страница 4

          ...                ... 

R=   ………………………………..…………..….....        

  ...               …

і вектор .

Нехай розв’язком цієї задачі є ₁⁰,..., _2n⁰. Тоді параметри моделі (4.19) визначаються як a_j=-_j⁰  і c_j=_n+j⁰  для j=1,2,…n.

Для оцінки якості отриманої моделі можна обчислити значення функціонала J(⁰). Якщо отримане число розглядається як мале, то задача розв’язана. Якщо ж ні, то збільшують n- порядок моделі і проводять нові обчислення.

Алгоритм Б.Хо При одержанні моделей методом найменших квадратів заздалегідь фіксується розмірність моделі. Може виявитися, що оптимальна модель має іншу розмірність.

Існує метод одержання моделей, розроблений Б.Л. Хо , який у випадку, коли відомо, що експериментальні дані відповідають лінійній системі невідомої розмірності, дозволяє встановлювати розмірність n її мінімальної моделі і знаходити відповідні матриці A, B, і C. Як вихідні дані розглядається реакція  зі стану спокою  для  на імпульсний вхідний вплив  для .

Передбачається, що існує лінійна  модель розмірності , що описує ці дані. Розшукується еквівалентна модель найменшої розмірності . Для цього будуються матриці і :

.

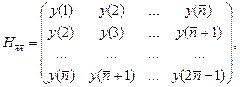
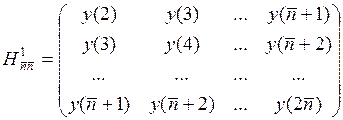Далі знаходяться такі невироджені матриці P і Q, для яких виконується , де  для  і  для .

Матрицю, яка стоїть  на перетині перших l рядків і перших m стовпців деякої матриці R, будемо позначати як .

Використовуючи це позначення, матриці еквівалентної моделі з простором станів мінімальної розмірності відповідно до алгоритму Б.Хо визначаються в такий спосіб:

,      і    .

Отже, число n, тобто число одиниць у діагональній матриці , є розмірністю мінімальної моделі. Ця модель є повністю керованою і повністю спостережуваною

Для систем зі скалярними входом і виходом задана модель , де a_n+1=1. Будемо вважати, що поліноми а₁+a₂λ+...+a_n+1λⁿ і c₁+с₂λ+. . .+c_nλ^n-1 не мають спільних нулів. Дискретна стаціонарна лінійна детермінована модель з простором станів має, як відомо, вигляд

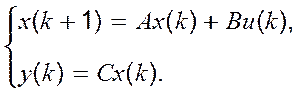              (4.22)

Стверджується, що така еквівалентна модель із простором станів може бути задана матрицями

A=Fb(-a₁, -a₂, ... , -a_n), В=е_п і С=(c₁,c₂,...,c_n).

Спочатку доведемо рівності:

φ_j (Fb(-a₁, ..., -a_n ))e_n =е_j для j=1,...,n,        (4.23)

де φ_j(λ) - похідні поліноми матриці Фробеніуса Fb(-a) .

Для j = п маємо (Fb(—a))e_n = Iе_n = е_п, тобто (4.23) виконано.

Припустимо за індукцією, що (4.23) виконане для j=п-1,п-2,...,l+1. Для j=l одержуємо

φ_l(Fb)e_n=Fb(-a)φ_l+1(Fb(-a))e_n+a_l+1Ie_n=Fb(-a)e_l+1+a_l+1e_n=

=(e_l–a_l+1e_n)+a_l+1e_n=e_l .

Тепер доведемо еквівалентність моделей. Оскільки Χ_A(λ)=Χ_Fb(-a)(λ)=a₁+a₂λ+...+λⁿ, то досить показати, що Cφ_j(A)B=c_j для всіх j. Маємо для j= 1,...,n

Cφ_j(A)B=(с₁,с₂, ..., c_n)φ_j(Fb(-a))e_n=(с₁, ..., с_n) е_j = с_j,

що і потрібно було довести.

Іншу модель із простором станів, що еквівалентна моделі (4.19), можна одержати за формулами

А=Fb*(-a), B=col(c₁, ..., c_n), C = e_n^*.  (4.24)

Дійсно, у лівій частині вхід-вихід моделі, еквівалентної моделі (4.24), коефіцієнти дорівнюють коефіцієнтам полінома

Χ_A=det(λI–Fb*(-a))=det(λI–Fb(-a))*=a₁+a₂λ+...+a_nλ^n-1+λⁿ,

тобто збігаються з коефіцієнтами моделі (4.19).

Обчислимо коефіцієнти правої частини вхід-вихід моделі, що відповідає моделі з матрицями (4.24). Маємо

Cφ_j(A)B=e_n*φ_j(Fb^*(-a))col(с₁,...,с_n)=

=(φ_j(Fb(-a)e_n)*col(с₁,...,с_n)=e_j*col(с₁, ..., с_n) = c_j,    (4.25)

тобто моделі (4.19) і (4.24) еквівалентні.

            Приклад. За відомою моделлю вхід-вихід

у(к+2)=-0.6у(к)-0.2у(к+1)+1.6u(к)+0.8u(к+1) побудувати модель з простором станів.

Розв’язання. Для моделі з простором станів

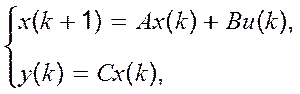
будуємо матриці A=Fb(-a₁, -a₂), В=е₂ і С=(c₁,c₂).

Використовуючи коефіцієнти заданої моделі вхід-вихід, будуємо

      .

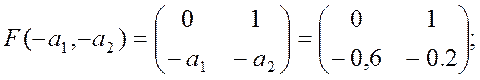
Тепер розглянемо задачу переходу від моделі (4.19) до моделі (4.22) для випадку dimu=m>1. У цьому випадку в (4.19) коефіцієнти с₁,...,с_n являють собою l×m - матриці й у (4.24) В є n×m - матрицею. Оскільки співвідношення (4.25) виконуються і у цьому випадку, то формули (4.24) дозволяють розв’язати задачу.