Исследование цепей синусоидального тока (Лабораторная работа № 4), страница 6

      1.5.1 Резонанс токов

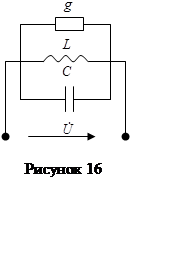
      Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными R, L и C (рис.16) При это воспользуемся результатами, полученными выше.

Комплексная проводимость такой цепи

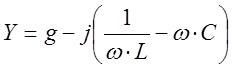      5.1

по своей структуре аналогична выражению 4.1, а резонансная частота определяется согласно 4.2. добротность резонансной цепи на основании 4.3

.

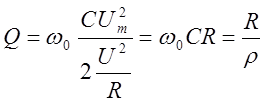По аналогии с предыдущим выражение 5.1 приводится к виду:

.

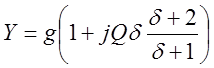Сравнивая полученный результат с 4.6 , убеждаемся, что выражение Y/g для схемы рисунок 16имеет тот же вид , что и выражение Z/R для схемы рисунок 11. поэтому кривые рисунок 12применимы и в данном случае.

Кривые рисунок 12.а показывают, что при резонансе токов полная проводимость цепи минимальна, т.е. входное сопротивление достигает максимума.

При заданном напряжении   на зажимах цепи ток, идущий от источника в цепь равен:

 .

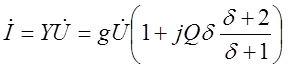величина этого тока достигает минимума при резонансной частоте, так как при этом

Следовательно, отношение величин токов  и определяется из выражения

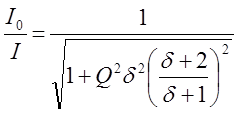, правая часть которого полностью совпадает с 4.8.

В связи с этим резонансные кривые (рисунок 13)выражают применительно к схеме на рисунке 16 зависимость /от δ. В случае резонанса токов токи в индуктивном и емкостном элементах схемы рисунок 16 равны по величине и противоположны по знаку:

.

Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и C по отношению к суммарному току  .

Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением  то чем меньше сопротивление , присоединяемое параллельно сопротивлению R, тем ниже добротность и шире полоса пропускания контура. Поэтому в отличие от последовательного колебательного контура с точки зрения сокращения полосы пропускания параллельного колебательного контура  выгоден источник тока с большим внутренним сопротивлением.

Схема рисунок 16 является идеализированной , так как она не учитывает активных потерь в ветвях L и C . Рассмотрим схемы с учетом активного сопротивления в ветвях L и C (рисунке 17).   

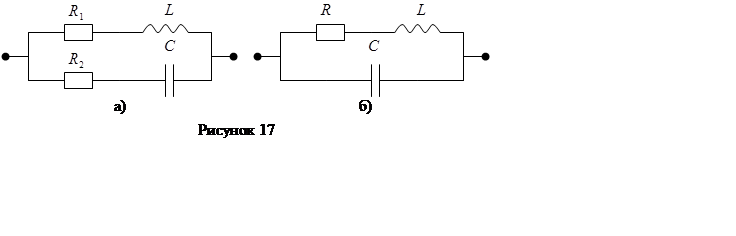Условие резонанса токов для схемы рисунок 17.а  записывается в виде равенства реактивных проводимостей: 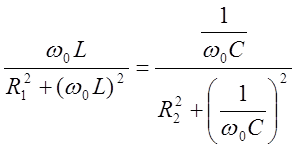        5.2 ,

откуда 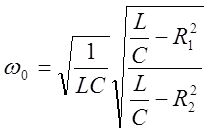 .       5.3

Явление резонанса возможно при этом только в том случае, если подкоренное выражение 5.3 имеет положительный знак. Если 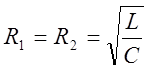, то цепь резонирует на любой частоте.

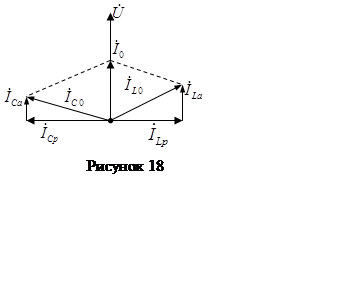            На рисунке 18 показана векторная диаграмма при резонансе токов в цепи (рис.17.а). Токи в индуктивной и емкостной ветвях слагаются из активных и реактивных составляющих, причем         

Чем меньше  по сравнению с  и 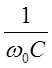 тем ближе к 180º угол фазового сдвига между , при этом токи  в ветвях образуют один контурный ток , замыкающийся в колебательном контуре. При резонансе вся цепь имеет только активную проводимость 

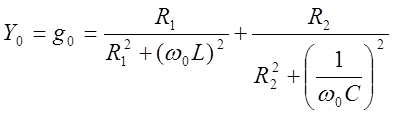, откуда с учетом 5.2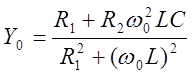  

Для колебательного контура с малыми потерями можно пренебречь слагаемым по сравнению с и считать, что  . При этом проводимость колебательного контура приближенно выразится формулой:

 .

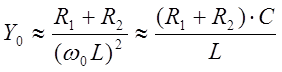При   согласно 5.3

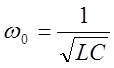   и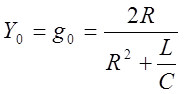   

легко убедиться в том, что и в случае резонансной цепи с двумя параллельными ветвями (рис.17) соблюдается условие  . Для этого достаточно умножить обе части уравнения 5.2  на  .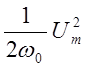

Для схемы рисунке 1.17.б при изменении частоты ω или индуктивности L минимум полной проводимости цепи, а также минимум общего тока наступают на при резонансной частоте. В том же случае, если переменным параметром является емкость C, проводимость и общий ток достигают минимума при резонансе токов.  

Добротность параллельного колебательного контура (рисунке 17.а)  на основании 4.3 равна

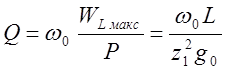, но 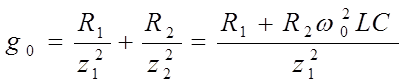 , откуда

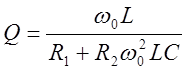, где резонансная частота определяется по формуле 5.3.

Для повышения крутизны резонансных характеристик, необходимой для более четкого разделения колебаний разных частот, широко применяются двухконтурные резонансные цепи: два резонансных контура, настроенных каждый в отдельности на одну и ту же частоту, связываются индуктивно или электрически. В отличие от одногорбой резонансной кривой одиночного контура в связанных цепях получаются двугорбые кривые: например, ток в каждом контуре может иметь максимумы при двух частотах, расположенных выше и ниже резонансной частоты одиночного контура.