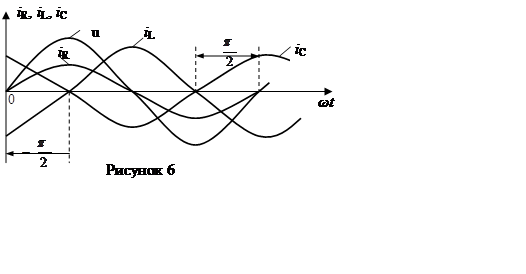
Ток ![]() в сопротивлении R
совпадает по фазе с напряжением u, ток
в сопротивлении R
совпадает по фазе с напряжением u, ток ![]() в индуктивности L отстает, а
ток
в индуктивности L отстает, а
ток![]() в ёмкости С опережает напряжение на
в ёмкости С опережает напряжение на
![]() (рисунок 6). Следовательно, суммарный ток i
в цепи равен :
(рисунок 6). Следовательно, суммарный ток i
в цепи равен :
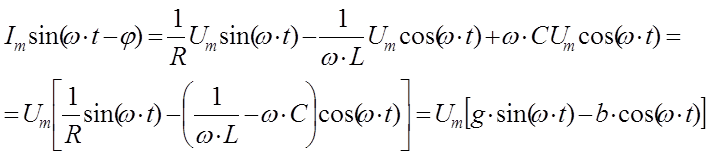 (1.80
(1.80
 |
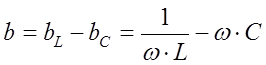 называется реактивной
проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b>0)
или емкостной (b<0) характер. Величина
называется реактивной
проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b>0)
или емкостной (b<0) характер. Величина 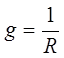 называется
активной проводимостью и всегда положительна.
называется
активной проводимостью и всегда положительна.
Для нахождения ![]() и φ
воспользуемся соотношениями 1.2 :
и φ
воспользуемся соотношениями 1.2 :
![]() ,
(1.9)
,
(1.9)
где 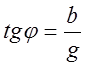 (1.10)
(1.10)
Из 1.9 следует, что ![]() ,
где
,
где
![]() (1.110
(1.110
-- полная проводимость, рассматриваемой цепи. Активная, реактивная и полная проводимости относятся к основным понятиям, применяемых в теории электрических цепей.
Согласно 1.10 ток i отстает от напряжения u на угол
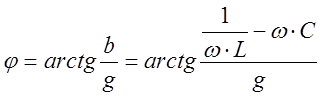 .
.
Если
задано напряжение ![]() на зажимах цепи с параллельно
соединёнными R,L и C , то ток определяется по
формуле:
на зажимах цепи с параллельно
соединёнными R,L и C , то ток определяется по
формуле:
![]() .
.
Угол φ, как и в предыдущем случае отсчитывается по оси углов ωtв направлении от напряжения к току и бывает острым или прямым:
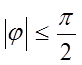 .
.
Угол φ положителен при индуктивном характере цепи (b>0) при этом ток отстает по фазе от напряжения .
Угол φ отрицателен при емкостном характере цепи (b<0) при этом ток опережает по фазе напряжение.
Ток
совпадает с напряжением по фазе при ![]() , т.е. при равенстве
индуктивного и емкостного проводимостей. Такой режим работы электрической цепи
называется резонансом токов. Из выражений 1.10 и 1.11 следует , что активное и
реактивное проводимости цепи связаны с полной проводимостью формулами :
, т.е. при равенстве
индуктивного и емкостного проводимостей. Такой режим работы электрической цепи
называется резонансом токов. Из выражений 1.10 и 1.11 следует , что активное и
реактивное проводимости цепи связаны с полной проводимостью формулами :
![]() . (1.12)
. (1.12)
Умножив правые и левые части выражений 1.12 на действующее значение напряжения U получим действующее значения токов в ветвях с активной и реактивной проводимостями, называемые активной и реактивной составляющими тока:
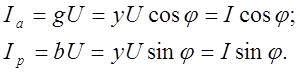 (1.13)
(1.13)
активная и реактивная составляющие тока связаны с
действующим значением суммарного тока формулой: ![]() .
.
Для характеристики конденсаторов, представляемых цепью с параллельным соединением элементов R и C , применяется понятие добротности конденсатора:
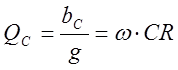 , которое равнозначно
тангенсу угла
, которое равнозначно
тангенсу угла ![]() конденсатора. Обратная величина
называется тангенсом угла диэлектрических потерь конденсатора
конденсатора. Обратная величина
называется тангенсом угла диэлектрических потерь конденсатора 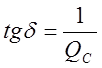 (угол диэлектрических потерь дополняет
угол
(угол диэлектрических потерь дополняет
угол![]() до 90º ).
до 90º ).
Чем больше сопротивление R, тем больше добротность конденсатора и тем меньше угол потерь. Добротность конденсаторов, применяемых в радиотехнике, автоматике и приборостроении определяется сотнями и тысячами (величина tg δ для разных частот и диэлектриков колеблется в пределах от 10-1 до 10-4).
1.3 Законы Ома и Кирхгофа в комплексной форме
Рассмотрим применение метода комплексных амплитуд в случае последовательного и параллельного соединений элементов R, L, C.
1.3.1 Последовательное соединение
Положим, что в уравнении Кирхгофа
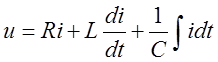 3.1
3.1
Заданными являются параметры R, L, C и
синусоидальное напряжение![]() на зажимах цепи, а
искомой величиной является ток i .Ввиду того, что здесь рассматривается установившийся
режим цепи синусоидального тока, решение этого дифференциального уравнения
должно дать синусоидальную функцию вида:
на зажимах цепи, а
искомой величиной является ток i .Ввиду того, что здесь рассматривается установившийся
режим цепи синусоидального тока, решение этого дифференциального уравнения
должно дать синусоидальную функцию вида:
![]() , где
, где
![]() , пока неизвестные
амплитуда и начальная фаза тока.
, пока неизвестные
амплитуда и начальная фаза тока.
Пусть заданное синусоидальное напряжение
символизируется заданной комплексной функцией ![]() , а
искомый синусоидальный ток – комплексной функцией
, а
искомый синусоидальный ток – комплексной функцией ![]() ,
комплексные амплитуды напряжения и тока соответственно:
,
комплексные амплитуды напряжения и тока соответственно:
![]() .
.
Сложение, дифференцирование и
интегрирование синусоидальных функций в уравнении 3.1 заменяются теми же
математическими операциями над мнимыми частями комплексных функций: 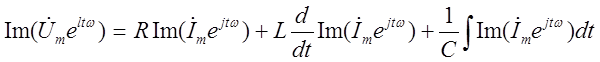
Операции над мнимыми частями
комплексных функций могут быть заменены операциями над самими комплексными
функциями с последующим выделением мнимой части полученного результата: 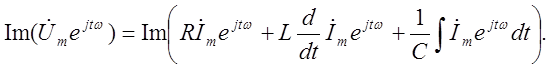
Полученное уравнение удовлетворяется для любого момента времени. Поэтому, заключенные в скобки комплексные выражения, от которых берётся мнимая часть, должны быть равны друг другу. Произведя дифференцирование и интегрирование, получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.