Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Тема 1

ВЫБОРКА И ЕЕ АНАЛИЗ

1  Выборка

2  Статистические ряды

3  Эмпирическая функция распределения и кумулятивная кривая

4  Лабораторная работа

1. Выборка. Пусть случайная величина  описывает количественный или качественный признак некоторого физического или экономического процесса. В реальных условиях обычно бывает трудно или экономически нецелесообразно, а иногда и невозможно, исследовать всю совокупность значений случайной величины (генеральную совокупность) исследуемого процесса. Поэтому на практике широко применяется выборочный метод, когда исследуется часть генеральной совокупности (выборочная совокупность или выборка). При этом выборка должна быть репрезентативной (представительной), что, в силу закона больших чисел, достигается случайностью отбора. Различают 5 основных типов выборок.

1. Собственно-случайная:

– повторная (элементы после выбора возвращаются обратно);

– бесповторная(выбранные элементы не возвращаются).

2. Типическая – генеральная совокупность предварительно разбивается на группы типических элементов, и выборка осуществляется из каждой. Следует различать:

– равномерная(при равенстве объемов исходных групп в генеральной совокупности выбирается одинаковое количество элементов из каждой);

– пропорциональная (численность выборок формируют пропорционально численностям или средним квадратическим отклонениям групп генеральной совокупности);

в) комбинированная (численность выборок пропорциональна и средним квадратическим отклонениям, и численностям групп генеральной совокупности).

3. Механическая – отбор элементов проводится через определенный интервал.

4. Серийная – отбор проводится не по одному элементу, а сериями для проведения сплошного обследования.

5. Комбинированная – используются различные комбинации вышеуказанных методов, например, типическая выборка сочетается с механической и собственно случайной.

2. Статистические ряды. Пусть из генеральной совокупности значений случайной величины  извлекается выборка  объема . Вариационным рядом называется таблица, в первой строке которой указываются варианты , , …,  наблюдаемого признака  в порядке возрастания , во второй строке – соответствующие им частоты  или относительные частоты

.

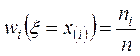Здесь  – количество наблюдений значения в выборке, .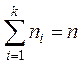

Таблица 1. Вариационный ряд

Варианты
Частота			…
Относительные частоты

Полигоном относительных частот (полигоном частот) называется ломаная линия, состоящая из отрезков, соединяющих точки 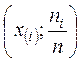 (точки ), .

При большом объеме выборки ее элементы могут быть сгруппированы в интервальный выборочный ряд (таблица 2). Для этого интервал изменения всех ее вариант разбивается на  непересекающихся полуинтервалов. Вычисления значительно упрощаются, если частичные интервалы имеют одинаковую длину 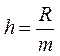, где величина  является размахом выборки. Количество интервалов – целая часть числа, определяемого по одной из формул: , ,  (формула Стерджесса). Затем подсчитывается число вариант выборки, попавших в каждый из интервалов, вычисляются относительные частоты числа вариант в интервале. Интервальный статистический ряд представляет собой таблицу, в первой строке которой указываются полуинтервалы , , , , во второй строке – соответствующие им частоты  или относительные частоты 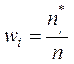, , где  – количество наблюдений в соответствующем интервале, 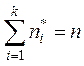,  – наибольшая варианта.

Таблица 2. Интервальный вариационный ряд

Варианты			…
Частота			…
Относительные частоты			…

Если серединам  каждого полуинтервала , , равной длины поставить в соответствие относительные частоты 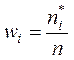, то получится вариационный ряд с равноотстоящими вариантами (таблица 3).

Таблица 3. Вариационный ряд с равноотстоящими вариантами

Варианты
Относительные частоты

Аналогично, для полуинтервалов разной длины получается вариационный ряд с неравноотстоящими вариантами.

Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, построенных на интервалах группировки , , так, что площадь каждого прямоугольника равна относительной частоте. Основание каждого прямоугольника лежит на оси  и равно длине полуинтервала, высота равна величине . Сумма площадей всех прямоугольников равна единице. Сортировка данных по убыванию частоты представляет собой отсортированную гистограмму.

Кумулятивной кривой (кумулянтой или кривой Лоренца) называется ломаная линия, соединяющая точки , .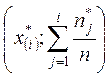

Полигон относительных частот можно рассматривать в качестве статистического аналога плотности распределения, а кумулятивную кривую – в качестве статистического аналога функции распределения.