Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 9

Задача анализа качества оценивания числовых характеристик случайного вектора  заключается в построении для них 0,5(m²+3m) доверительных интервалов

,   ,

,   ,

,   ,  j < l

и вычислении такого же числа доверительных вероятностей:

,   ,

,   ,

,   ,  j < l.

Методики анализа точности и надёжности оценивания числовых характеристик положения (математических ожиданий и рассеяния (дисперсий и средних квадратических отклонений) были подробно рассмотрены в § 5.2. Поэтому здесь основное внимание будет уделено анализу качества оценивания числовых характеристик связи (корреляционных моментов и коэффициентов корреляции) компонент случайного вектора .

При k_n–1 » 1 точечные оценк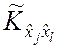и  и  вычисляются соответственно по третьей формуле (5.3.6) и (5.3.7). Известно, что корреляционный момент кроме связи компонент случайного вектора  характеризует и их рассеяние. Поэтому в качестве основной характеристики связи чаще всего используется коэффициент корреляции .

При вычислении доверительной вероятности b = b_I, n и построении доверительного интервала I = I_b,n для коэффициента корреляции необходимо знать закон распределения его оценки . Оказывается, что независимо от распределения случайного вектора  при достаточно большом объёме n выборки (практически при n > 30) закон распределения оценки  близок к нормальному [1] с параметрами

                                           ,    ,                       

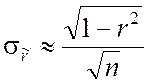иначе

                              .          

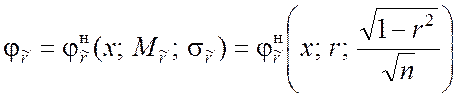Поэтому доверительная вероятность

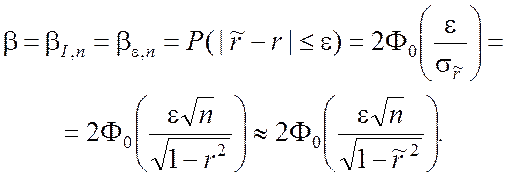                                                                                   (5.3.8)

Выражая из уравнения (5.3.8) величину e, будем иметь

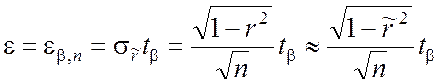                               , (5.3.9)

откуда

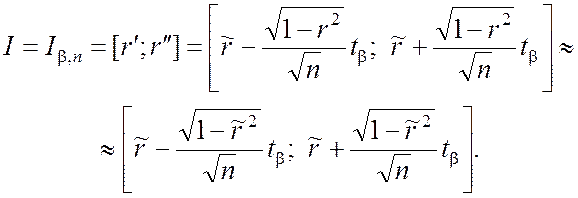                                                                             (5.3.10)

Соотношением (5.3.10) описывается 100b-процентной доверительный интервал для коэффициента корреляции r.

Разрешив уравнение (5.3.9) относительно n, получим выражение для объёма выборки, потребного при оценивании r с точностью e (с абсолютной ошибкой, не превосходящей e) и надёжностью b (доверительной вероятностью b):

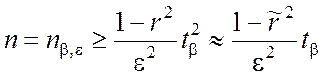                                       .        (5.3.11)

Следует обратить внимание на то, что во всех выражениях (5.3.8)–(5.3.11) реальными являются лишь приближённые равенства, так как на этапе оценивания (как точечного, так и интервального) истинное значение коэффициента корреляции неизвестно. В связи с этим потребный объём выборки может быть определён лишь методом последовательных приближений. Сущность этого метода была раскрыта в п.п.5.2.3.

П р и м е р 5.10. Пусть ,  – координаты пробоины в мишени. Произведено 40 выстрелов. Коэффициент корреляции случайных величин  и  составил r = 0,605. Найти:

1) доверительную вероятность b для r, если максимальная с вероятностью b абсолютная погрешность оценки  должна быть не более 0,1;

2) доверительный интервал для r при доверительной вероятности b = 0,85.

▼ 1. По формуле (5.3.8) находим

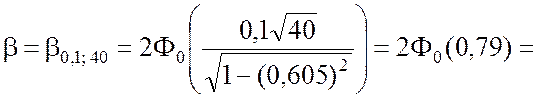0,5704.

Значение функции F₀(x) – в приложении 2.

2. Для b = 0,85 в приложении 4 находим t_b = t_0,85 = 1,439.

Для вычисления погрешности e используем выражение (5.3.9):

                               .

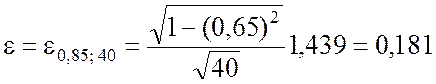В соответствии с выражением (5.3.10) доверительный интервал

          I = I_0,85; 40 = [0,605–0,181;   0,605+0,181] = [0,424;   0,786].

                                                                                                       ▲

5.4. Оценивание числовых характеристик случайных функций

Известно, что случайная функция может рассматриваться как обобщение понятия случайного вектора (системы случайных величин) на бесконечное множество составляющих его компонентов (сечений случайной функции). Исчерпывающего вероятностного описания такого случайного объекта не существует, поэтому на практике используются лишь законы распределения и числовые характеристики систем конечного числа сечений случайных функций. При этом из-за сложности построения статистических законов распределения многомерных случайных векторов наиболее широкое применение получила корреляционная теория, в рамках которой изучаются лишь первые и вторые моменты распределений случайных функций, т.е. их математические ожидания, дисперсии и корреляционные функции.