Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 2

▲

Следует обратить внимание на то, что выборка, приведённая в табл.4.7, принадлежит той же генеральной совокупности, что и в табл.4.3. Однако, как видно из решений примеров 5.1 и 5.2, в последнем случае даже приближённое значение оценки  меньше отличается от истинного значения параметра  = 100 ч. Это объясняется бо́льшим объёмом n и, следовательно, большей информативностью выборки, приведённой в табл.4.7.

5.1.2. Неравноточные наблюдения

Пусть характеристики точности наблюдений от опыта к опыту изменяются так, что наблюдаемая в i-м опыте случайная величина  имеет дисперсию

                                               ,   .

При этом среднее значение случайной величины  от опыта к опыту не изменяется:

                                           ,   .

В данном случае оценка  математического ожидания случайной величины  по-прежнему будет являться функцией случайной выборки:

                                                 .

Необходимо так выбрать вид этой зависимости, чтобы оценка имела простое аналитическое выражение и была несмещённой, состоятельной и эффективной.

Так как наиболее простой функциональной зависимостью является линейная, то будем искать оценку  в классе линейных функций:

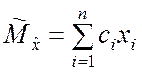                                                    .                       (5.1.5)

Очевидно, что теперь решение поставленной задачи состоит в отыскании значений коэффициентов c_i,  линейной формы (5.1.5), при которых оценка  будет удовлетворять всем трём указанным выше требованиям.

1. Чтобы оценка была несмещённой, должно выполняться равенство

                                                   .

Поскольку в этом случае

,

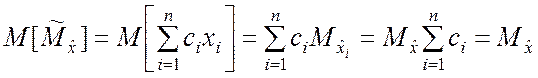то коэффициенты c_i должны удовлетворять условию

.

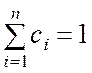2. Для того чтобы оценка  была эффективной, её дисперсия

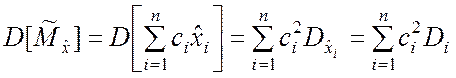                              (5.1.6)

должна быть минимальной при условии, что

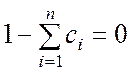                                                     .                        (5.1.7)

 Условный экстремум (минимум) функции (5.1.6) с переменными  c₁,  c₂,…, c_n  отыскиваем методом неопределённых множителей Лагранжа. При этом учитываем, что должно выполняться равенство (5.1.7). Следовательно, исследуем на минимум вспомогательную функцию                

                       ,   

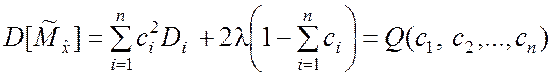где l – неопределённый множитель Лагранжа.

Решаем систему n уравнений

                                       ,   

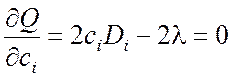относительно переменных  c₁,  c₂,…, c_n  и получаем

                                                        .

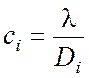Таким образом, вес c_i, с которым должен входить результат i-го наблюдения в формулу для оценки , должен быть обратно пропорционален его дисперсии. Иными словами, чем точнее наблюдение, тем с бо́льшим весом необходимо учитывать его результат. Вывод, полученный формально, полностью согласуется с вербальными рассуждениями: чем точнее наблюдение, тем больше ему следует доверять.

Поскольку 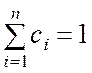,  то 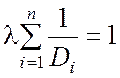   и, следовательно,

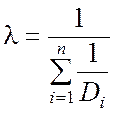                                                      .                         (5.1.8)

Обозначим  1/D_i = d_i, тогда  (5.1.8)  представляется  как 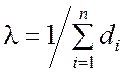   и

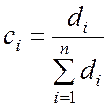                                              ,    .                 (5.1.9)

Таким образом, выражение для оценки  (5.1.5)   будет иметь вид

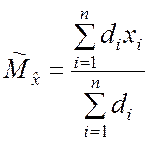                                                    .                    (5.1.10)

Оценка вида (5.1.10) является эффективной, так как получена на основе требования минимума дисперсии.

3. Минимальная дисперсия несмещённой оценки

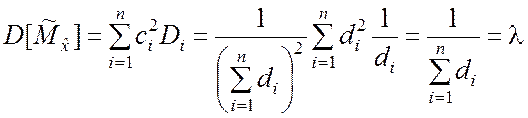                         ,                                                        (5.1.11)

а её среднее квадратическое отклонение

                                             .

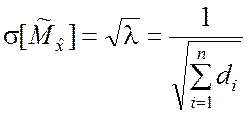Поскольку d_i = 1/D_i = const,  , то из выражения (5.1.11) вытекает, что при неограниченном возрастании количества наблюдений l ® 0. Следовательно,  сходится по вероятности к , т.е. является состоятельной оценкой математического ожидания .

Частный случай. Предположим, что все наблюдения равноточны. Это означает, что  ,  ,  ,    и тогда