Реализации xi(t), ![]() случайной
функции
случайной
функции ![]() представляют собой неслучайные функции,
значения которых xi(tj) в фиксированных точках tj, j = 1,2,… являются реализациями
xij случайных величин
представляют собой неслучайные функции,
значения которых xi(tj) в фиксированных точках tj, j = 1,2,… являются реализациями
xij случайных величин ![]() .
.
Пусть над случайной функцией ![]() произведено
n независимых равноточных наблюдений (опытов), в
результате которых получено n её реализаций xi(t),
произведено
n независимых равноточных наблюдений (опытов), в
результате которых получено n её реализаций xi(t), ![]() (рис.5.3).
(рис.5.3).
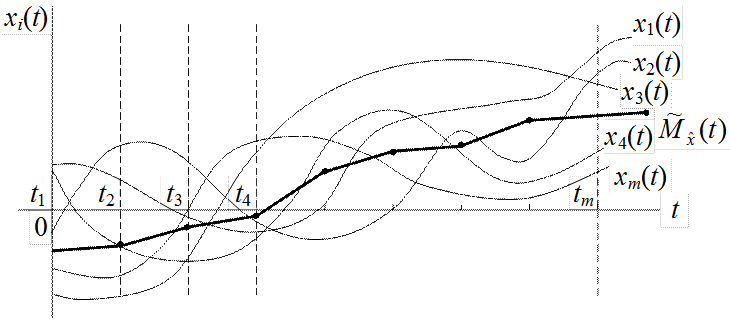
Рис.5.3. Реализации случайной функции
Требуется найти оценки числовых характеристик случайной функции:
математического ожидания ![]() , дисперсии
, дисперсии ![]() и корреляционной функции
и корреляционной функции ![]() , удовлетворяющие требованиям
состоятельности, несмещённости и эффективности (асимптотической эффективности).
, удовлетворяющие требованиям
состоятельности, несмещённости и эффективности (асимптотической эффективности).
В ряде сечений случайной функции, соответствующих моментам
времени t1, t2,…,
tj,…,tm,
фиксируются значения, принятые реализациями xi(t) функции ![]() в эти моменты.
Поскольку наблюдалось n реализаций, то каждому
из моментов tj,
в эти моменты.
Поскольку наблюдалось n реализаций, то каждому
из моментов tj, ![]() будут соответствовать n
значений, принятых случайной величиной
будут соответствовать n
значений, принятых случайной величиной ![]() .
Указанная случайная величина является j-м
сечением случайной функции
.
Указанная случайная величина является j-м
сечением случайной функции ![]() . Расстояния
. Расстояния
h = hj = tj+1 – tj
между фиксируемыми сечениями ![]() случайной
функции
случайной
функции ![]() обычно берутся одинаковыми и назначаются
так, чтобы последовательность xi(tj),
обычно берутся одинаковыми и назначаются
так, чтобы последовательность xi(tj), ![]() позволяла
восстановить основной характер зависимости xi(t). Нередко в основу выбора кладётся теорема
В.А. Котельникова, согласно которой для точного восстановления непрерывной
функции достаточно её наблюдать в равноотстоящих дискретных точках с частотой,
в два раза превышающей максимум её частотного спектра [2,13]. Бывает, что приведённые
соображения являются излишними и расстояние задаётся темпом работы
регистрирующей аппаратуры.
позволяла
восстановить основной характер зависимости xi(t). Нередко в основу выбора кладётся теорема
В.А. Котельникова, согласно которой для точного восстановления непрерывной
функции достаточно её наблюдать в равноотстоящих дискретных точках с частотой,
в два раза превышающей максимум её частотного спектра [2,13]. Бывает, что приведённые
соображения являются излишними и расстояние задаётся темпом работы
регистрирующей аппаратуры.
Для удобства последующей статистической обработки зарегистрированные данные сводятся в таблицу, строки которой соответствуют реализациям, а столбцы – сечениям случайной функции (табл.5.6).
Таблица 5.6
Зарегистрированные значения случайной функции
|
xi(t) |
t |
|||||||
|
t1 |
t2 |
××× |
tj |
××× |
tl |
××× |
tm |
|
|
x1(t) |
x1(t1) |
x1(t2) |
××× |
x1(tj) |
××× |
x1(tl) |
××× |
x1(tm) |
|
x2(t) |
x2(t1) |
x2(t2) |
××× |
x2(tj) |
××× |
x2(lj) |
××× |
x2(tm) |
|
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
|
xi(t) |
xi(t1) |
xi(t2) |
××× |
xi(tj) |
××× |
xi(tl) |
××× |
xi(tm) |
|
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
|
xn(t) |
xn(t1) |
xn(t2) |
××× |
xn(tj) |
××× |
xn(tl) |
××× |
xn(tm) |
Приведённая в табл.5.6 совокупность значений случайной функции ![]() представляет собой результаты n наблюдений m-мерного
случайного вектора
представляет собой результаты n наблюдений m-мерного
случайного вектора
![]()
и обрабатывается по методике § 5.3.
Так, оценки математических ожиданий сечений ![]() случайной функции
случайной функции ![]() находятся
по формулам
находятся
по формулам
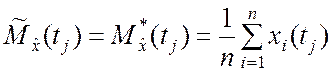 ,
, ![]() . (5.4.1)
. (5.4.1)
Соединяя точки ![]() отрезками прямых,
можно построить приближённый график (рис.5.3) оценки
отрезками прямых,
можно построить приближённый график (рис.5.3) оценки ![]() математического
ожидания
математического
ожидания ![]() случайной функции
случайной функции ![]() .
Очевидно, что возможны и другие виды интерполяции, например, квадратичная.
.
Очевидно, что возможны и другие виды интерполяции, например, квадратичная.
Несмещенные оценки дисперсий и корреляционных моментов сечений определяются соответственно следующими соотношениями:
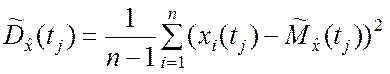 ,
, ![]() . (5.4.2)
. (5.4.2)
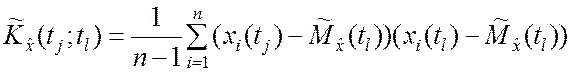 ,
, ![]() . (5.4.3)
. (5.4.3)
Легко заметить, что формула (5.4.2) может быть получена и из
выражения (5.4.3) при l = j, поскольку ![]() .
.
В вычислительном отношении более удобны формулы, основанные на связи начальных и центральных моментов, т.е.
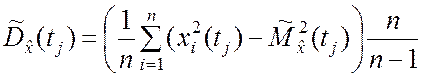 ,
, ![]() . (5.4.4)
. (5.4.4)
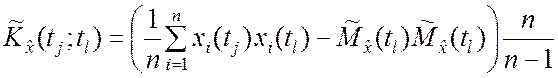 ,
, ![]() . (5.4.5)
. (5.4.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.