Магнитная гидродинамика, страница 6

 .                              (13.2.21)

Тогда в магнитной гидродинамике вектор плотности потока полной энергии будет иметь вид:

 .

В формуле (13.2.21)  может быть выражена через  при помощи уравнений 1,5 системы(13.1.6). Имеем:

 .

Подставляя последнее выражение в (13.2.21) и добавляя полученное к правой части (13.2.20) имеем:

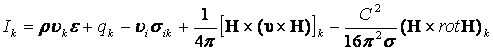.    (13.2.22)

Выражение (13.2.22) представляет собой вектор Умова – вектор плотности потока полной энергии в магнитной гидродинамике. Поскольку плотность магнитной энергии единицы объема равна, то полная энергия единицы объема в магнитной гидродинамике будет равна: 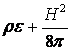. Поэтому закон сохранения полной энергии запишется в виде:

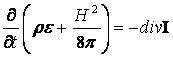 .                             (13.2.23)

Где вектор  определен выражением (13.2.22).

Трудность понимания процессов, происходящих в проводящей жидкости, движущейся в магнитном поле, заключается в том, что здесь нарушаются обычные причинные связи, известные нам из лабораторной практики.

В обычной лабораторной практике причинная связь явлений заключается в следующем: некоторая ЭДС определяет электрический ток, ток в свою очередь определяет магнитное поле и т.д.

В магнитной гидродинамике причинная связь чаще следующая: движущаяся жидкость изменяет магнитное поле, изменение магнитного поля, согласно уравнениям Максвелла, вызывает электрическое поле, определяющее ток, который, в свою очередь, создает магнитное поле, влияющее на движение жидкости.

13.3. Принцип вмороженности магнитных силовых линий

 Рассмотрим принцип, формулировка и доказательство которого принадлежит Альфену. Этот принцип играет большую роль в создании тех немногих образных представлений, которые возможны в магнитной гидродинамике.

 Рассмотрим уравнение (13.2.18):

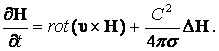
Если проводимость  - очень велика, то последним членом в уравнении (13.2.18) можно пренебречь. Таким образом, при  из уравнения (13.2.18) получаем следующее уравнение:

 .                                      (13.3.24)

Преобразуем правую часть уравнения (13.3.24):

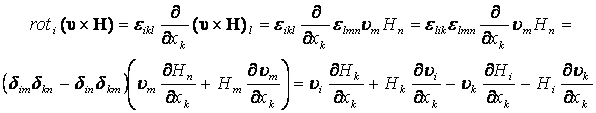
Из последнего соотношения следует векторная формула:

 .

Поскольку , то уравнение (13.3.24) можно переписать в виде:

 .                (13.3.25)

Из уравнения непрерывности имеем:

 .

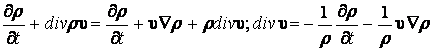Подставляя последнее выражение в (13.3.25), получим:

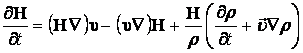 .            (13.3.26)

Рассмотрим выражение:

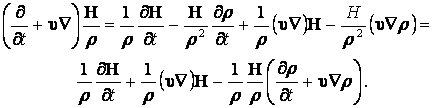       (13.3.27)

Комбинируя (13.3.27) и (13.3.26) получим:

 .

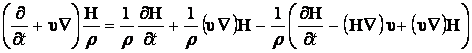Сократив члены в последнем выражении имеем:

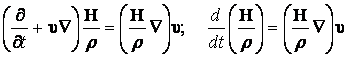          .             (13.3.28)

Рассмотрим смысл полученного выражения, Пусть в жидкости имеется некоторая “жидкая” линия то есть линия, состоящая из одних и тех же частиц (см. рис. 2):