Спецглавы математики: Сборник задач и упражнений, страница 8

Для решения задач из этого раздела необходимо проработать теоретический материал из [7, с. 9-62]. В данном сборнике задач используется следующая терминология.

k-расстановка – всякое упорядоченное или неупорядоченное множество, содержащее k элементов.

k-размещение из n элементов (размещение из n элементов по k) – упорядоченная k-расстановка, составленная из элементов n-элементного множества
(k £ n). Два k-размещения из элементов одного и того же множества отличаются друг от друга составом или порядком следования элементов; число таких размещений определяется формулой

n-перестановка (перестановка из n элементов) – частный случай k-раз-мещения из n элементов, когда k = n, иначе говоря, это n-размещение из n элементов. Две n-перестановки из элементов одного и того же множества отличаются друг от друга только порядком следования элементов. Число n-переста-новок определяется формулой

P_n = n!                                            (3.2)

  k-сочетание из n элементов (сочетание из n элементов по k) – всякая неупорядоченная k-расстановка, являющаяся подмножеством n-элементного  множества (k £ n). Два сочетания из элементов одного и того же множества могут отличаться друг от друга только составом элементов (порядок следования элементов значения не имеет). Число k-сочетаний из n элементов определяется формулой

В отличие от обычных множеств, где все элементы считаются различными, k-расстановки могут содержать одинаковые элементы, иначе говоря, элементы неразличимые или эквивалентные с точки зрения решаемой задачи. Такие k-расстановки называются k-расстановками с повторениями.

Если k-расстановка с повторениями может включать в себя элементы n различных типов и упорядочена, то она называется k-размещением с повторениями из элементов n типов (размещением с повторениями из элементов n типов по k). Число таких размещений

n-перестановка, включающая в себя элементы k различных типов, причем число элементов каждого типа (n_i) задано, называется n-перестановкой с повторениями из элементов k типов. Число таких перестановок

 

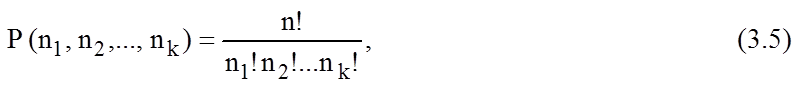
где n₁ + n₂ + … + n_k  = n.

Неупорядоченная k-расстановка с повторениями, которая может включать в себя элементы n типов, называется k-сочетанием с повторениями из элементов n типов (сочетанием с повторениями из элементов n типов по k). Число таких сочетаний

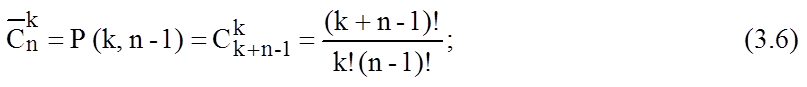
При решении комбинаторных задач, предлагаемых в данном разделе, в первую очередь необходимо обращать внимание не то, нельзя ли множество расстановок, рассматриваемых в задаче, разбить на взаимно не пересекающиеся подмножества, число расстановок в каждом из которых можно определить по известным правилам. Если это сделать можно, то применяют правило суммы, отражающее тот очевидный факт, что общее число элементов множества, разбитого на непересекающиеся подмножества, равно сумме чисел элементов всех этих подмножеств.

Очень важно верно определить, к какому из перечисленных выше видов относятся выделенные расстановки. При этом, как видно из вышеприведенных определений, следует обращать внимание на то, имеет ли значение порядок следования элементов в расстановках, могут ли повторяться в одной расстановке одни и те же элементы и, если расстановки упорядочены, то все ли возможные элементы (или типы элементов) используются в каждой из них.

Процедуру определения типа расстановки можно представить в виде следующей таблицы:

Порядок следования элементов	Возможность повторения элементов в расстановке
	нет		да
не имеет значения	сочетание		сочетание с повторениями
имеет значение	Использование элементов		Использование типов элементов
	не все	все	не регламентируется, любые из имеющихся	количество элементов каждого типа задано
	размещение	перестановка	размещение с повторениями	перестановка с повторениями

Если расстановка упорядочена и известно количество способов, которыми можно выбрать каждый ее элемент, причем количество вариантов выбора данного элемента не зависит от того, как были выбраны предыдущие элементы, то для определения числа таких расстановок можно воспользоваться правилом произведения, в соответствии с которым число таких расстановок равно произведению чисел вариантов выбора всех входящих в расстановку элементов.