Спецглавы математики: Сборник задач и упражнений, страница 5

1.30.  Какими свойствами обладают отношения (X, R) и (X, R^-1), если:
а) Х – множество геометрических фигур; R = {(x, y)| фигура х подобна у};
б) Х – множество прямых на плоскости; R = {(x, y)| x||y};
в) Х – то же, что и в б); R = {(x, y)| прямая х перпендикулярна у};
г) Х – множество окружностей на плоскости; R = {(x, y)| окружность х 
    концентрична окружности у};
д) Х – то же, что и в г); R = {(x, y)| окружность х  касается окружности у};
е) Х = N – множество натуральных чисел; R = {(m, n)| m без остатка де-  
    лится на n);
ж) Х = Е – множество действительных чисел; R = {(x, y)| x £ y};
з)  Х – то же, что и в ж); R = {(x, y)| x < y};
и) X = Z – множество целых чисел; R = {(x, y)| x – y делится без остатка
    на р, где р – натуральное число}.

1.31.  Какими свойствами обладают отношения (X, R) и (X, R^-1), где Х - множество людей, если:
а) R = {(x, y)| х моложе у};
б) R = {(x, y)| х ребенок у};
в) R = {(x, y)| х состоит в браке с у};
г) R = {(x, y)| х живет в одном городе с у};
д) R = {(x, y)| х брат у};
е) R = {(x, y)| х похож на у};

1.32.  Найдите среди отношений, приведенных в упражнениях 1.30, 1.31, отношения эквивалентности, частичного порядка, строгого частичного порядка. Какие из множеств, на которых заданы отношения порядка, линейно упорядочены?

2.  ТЕОРИЯ ГРАФОВ

Теоретический материал, необходимый для решения задач данного раздела, можно найти в пособиях [5, с. 44-57, 6, с. 67-83, 5, с. 15-19, 28-37, 64-65]. В соответствии с терминологией, принятой в учебном пособии [5], в дальнейшем отрезок, соединяющий вершины неографа, будем называть звеном, тогда как термин ребро будем использовать для обозначения объединения понятий звено и дуга. Будем пользоваться также следующим определением композиции графов, согласованным с принятым в работе [5] определением композиции соответствий.

Композицией графов G₁ = (X, Г₁) и G₂ = (X, Г₂), заданных на одном и том же множестве вершин, называется граф G = (X, Г), заданный на том же множестве вершин, в котором Г = Г₁○ Г₂. Последнее означает, что в графе G дуга
(x_i, x_j) существует тогда и только тогда, когда можно построить путь длины 2, начинающийся в x_i и заканчивающийся в x_j, такой, что первая дуга этого пути принадлежит графу G₁, а вторая – графу G₂. Композицию графов G₁ и G₂ будем обозначать G₁○G₂. Матрица смежности композиции графов определяется как булево произведение матриц смежности исходных графов:

М(G₁○G₂) = М(G₁)М(G₂).

Если G₁ и G₂ – мультиграфы, то кратность ребра (x_i, x_j) в композиции G₁○G₂ равна числу путей длины 2 из вершины x_i в вершину x_j, удовлетворяющих указанным выше условиям, а матрица смежности композиции определяется обычным произведением матриц смежности исходных мультиграфов.

В ряде практических приложений теории графов важную роль играет решение вопроса о связности (сильной связности) графа и всех его связных компонент или (для орграфов) максимальных сильно связных подграфов. Последняя задача может быть решена, например, с помощью алгоритма, предложенного Мальгранжем [8, c. 164-168], или ему подобных [9, c. 29-36]. Эти алгоритмы могут быть использованы после некоторого упрощения также для выделения связных компонент в неографах.  Действительно, если связная компонента неографа содержит вершину x_i, то множество вершин этой компоненты С(x_i) совпадает, очевидно, с множеством вершин, достижимых из вершины x_i:

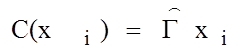. Остальные операции выполняются так же, как в алгоритме Мальгранжа.

Важное практическое значение имеют также многие экстремальные задачи на графах (отыскание кратчайших и длиннейших путей [8, c. 281-284; 10, c. 19-22; 5, c. 51-56; 6, c. 76-83], минимального каркаса [5, c. 57-58], максимального потока [5, c. 58-64]).

Пример 2.1. В графе G = (X, Г), заданном матрицей смежности M(G), найти все максимальные сильно связные подграфы.  

Является ли граф G связным? сильно связным?