Окислительно-восстановительные электрохимические системы, страница 3

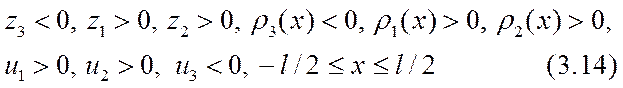
Второй этап решения системы уравнений (3.1) — (3.3) целесообразно начать с подробной записи оставшихся четырех уравнений:

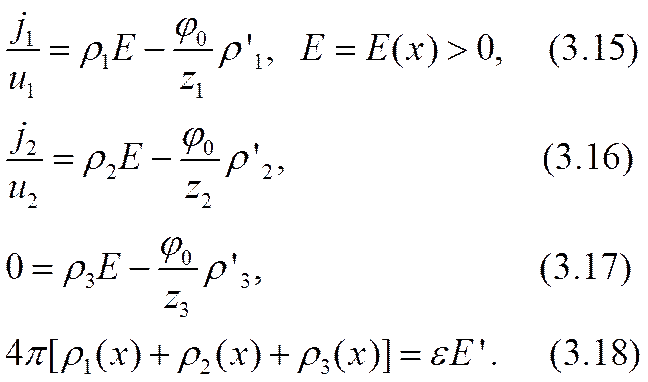
Неизвестные функции от координаты считаются ограни­ченными, непрерывными с нужным числом своих произ­водных, интегрируемыми нужное число раз и сохраняю­щими указанные им знаки (3.14), не проходя через нуль. Краевые условия для системы уравнений (3.15) — (3.18)   ограничены   неравенствами   (3.14)   и   известны в интегральной  форме:

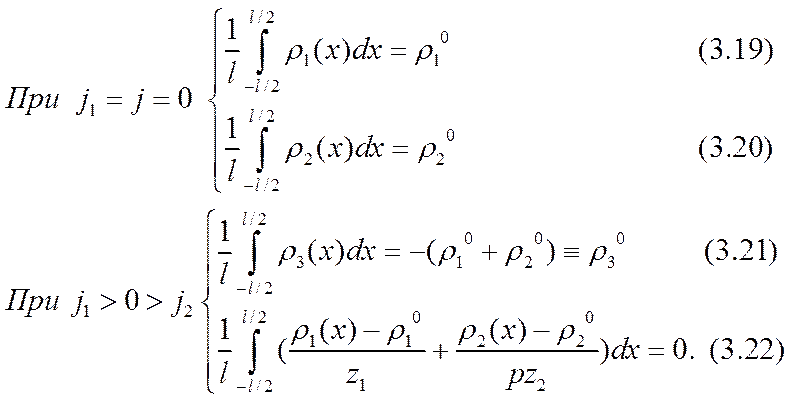
Здесь первые два условия (3.19) и (3.20) неоднородны, их правые части определяются технологией приготовления электролита; суммарные объемные заряды (на единицу площади электродов) всех ионов первого и второго сорта как в ионизованном, так и связанном состояниях известны. Третье условие (3.21) отображает первоначальную электро­нейтральность образца раствора в момент его приготов­ления до включения электрического поля. Через r⁰₃ здесь обозначен средний по межэлектродному промежутку объемный заряд третьей, пассивной ионной компоненты электролита. Четвертое условие (3.22), основанное на фор­мулах (3.9) — (3.12), отражает закон сохранения вещества активных ионов в пределах межэлектродного промежутка.

В процессе решения системы (3.15) — (3.18) проще всего исключается функция Е (х), входящая в первые три уравнения (3.15) — (3.17) только алгебраически и притом линейно. Из уравнения (3.17) значение Е (х) определяется через пока неизвестное распределение объемного заряда пассивной компоненты r₃ (х):

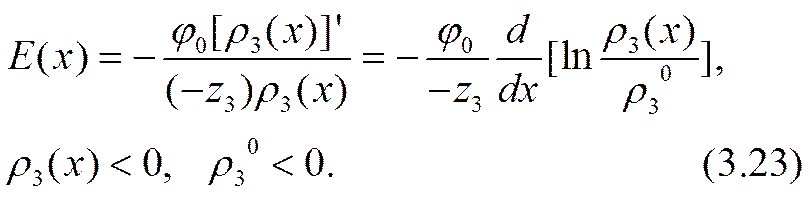
Подстановка значений Е (х) в уравнения (3.15) и (3.16) позволяет рассматривать их теперь как обыкновенные линейные неоднородные уравнения первого порядка относительно плотностей зарядов активных компонент:

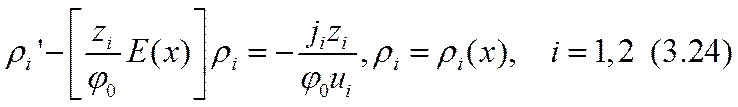
Эти уравнения имеют известные решения, в которые входят вспомогательные функции
Р (х) = P_i(х), Q_i и произволь­ные постоянные С = C_i, С₁ = С_i1, С₂ = C_i2, . . ., C_im, а также валентности ионов z = z (i), парциальные плот­ности токов j = j_i и т. п. (индексы i и m пока опущены):

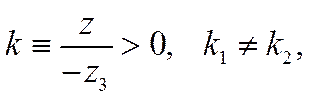
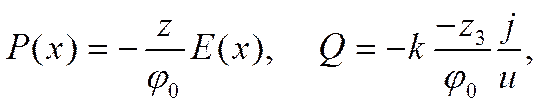
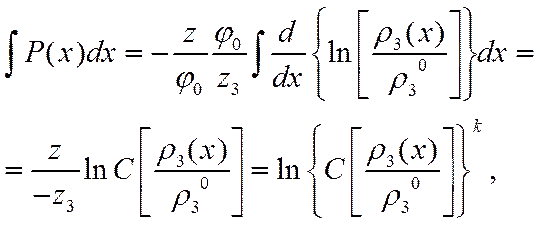
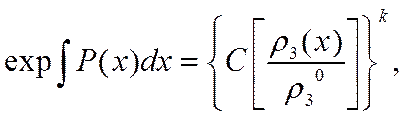
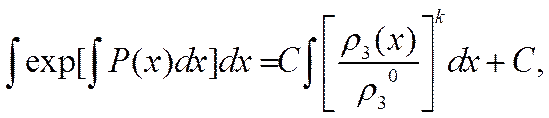
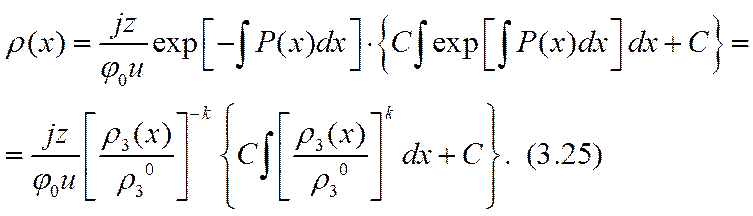
Предстоит выписать также решения для каждой из двух активных компонент раствора, подставить их в формулу Остроградского — Гаусса (3.18) и подобрать вид функции р₃ (х) и значения постоянных C_im, удовлетворяющих этому замыкающему уравнению системы (3.15) — (3.18). Запись (3.25) решения для r* (х) указывает на сложность этих операций и малую перспективность точного аналитиче­ского решения нелинейной задачи. Приходится обратиться к приближенным приемам, например к методу последова­тельных приближений. Успех метода обычно определяется Удачей выбора нулевого приближения, а для сокращения вычислений полезны искусственные приемы.

На основании опыта решения задачи о бинарном электролите   в    плоскопараллельной    ячейке   (гл.   2, формула (2.47)) целесообразно испытать в качестве нулевого приближения приближение Планка 12.01, т. е. линейную зависимость s =s (x) или r₃  = r₃  (х) по формуле (2.5), например:

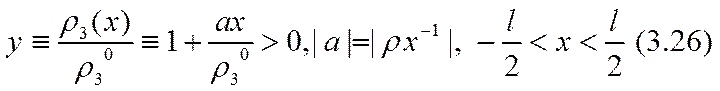
тогда формула (3.25) сразу приобретает простой вид:

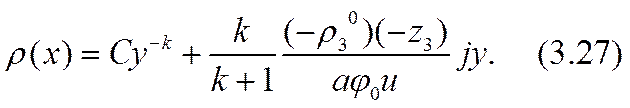
Решения (3.27) уравнений (3.24) должны удовлетворять неравенствам (3.14). Из соотношений (3.23) и (3.26) выте­кают в этом приближении формулы

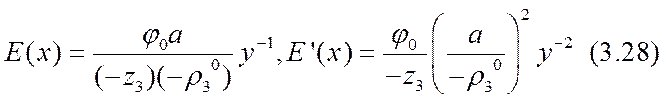
Из уравнения Остроградского — Гаусса для этого нулево­го приближения получается структура функциональной зависимости (х):

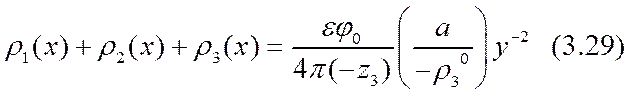
Подстановка значений r_i (х), взятых из формул (3.27) и (3.29), в соотношения (3.4), (3.13) и (3.18) приводит к составлению замыкающего уравнения для приближе­ния (3.26)

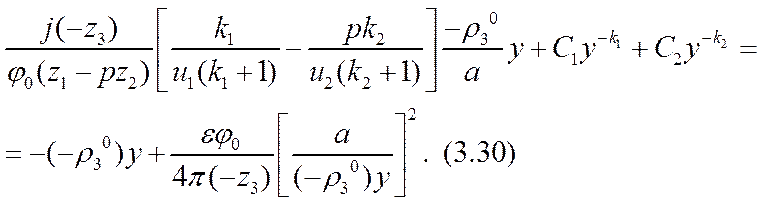
Здесь четвертое краевое условие (3.22) удовлетворено автоматически. Объединения произвольных постоянных интегрирования С_i с постоянными параметрами u_i, z_i обозначенные символами C_im, позволяют упростить вид уравнения (3.30):