Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 20

     Выделяют огибающую , полную фазу и фазовую функцию . Используя модель (1.14) обычно предполагают, что огибающая и фазовая функция  изменяются незначительно за время 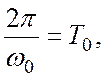 т.е.за период несущей частоты сигнала. Если огибающая  — финитная функция, то радиосигнал (1.14) называют радиоимпульсом, огибающую  соответствующим ему видеоимпульсом, а — частотой заполнения, или несущей частотой  радиоимпульса. Выбрав в качестве огибающей прямоугольный видеоимпульс получим радиосигнал в виде прямоугольного радиоимпульса:

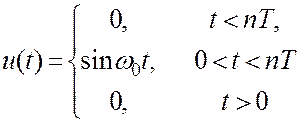                                                                                           (1.15)

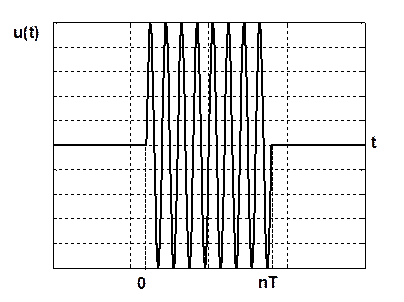
                             Рис.1.10. Осциллограмма прямоугольного радиоимпульса

   Очевидно, что его огибающая соответствует видеоимпульсу (1.4). Аналогичный сигнал мы уже рассматривали выше, см. формулу (3.41) Раздела 3 данного описания, она обобщает понятие радиоимпульса на случай произвольною функции огибающей .

   Этот пример  важен  для практических приложений. Если число периодов заполнения  радиоимпульса неограниченно растет, (а это означает, кстати, что и длительность сигнала неограниченно увеличивается), то спектр его превращается в дельта – функцию в области положительных и отрицательных частот.  (  формула (3.40) Раздела 3). Если заполнение сигнала формируется не одним гармоническим процессом, а двумя – с частотами и , то эти частоты могут быть разделены. Иными словами, здесь мы имеем дело с идеальной разрешающей способностью спектрального анализа.

   Напротив, если число периодов несущей частоты невелико, и опять в сигнале присутствует второй гармонический сигнал со своей несущей, то расфильтровать эти несущие поодиночке тем труднее, чем меньше их периодов укладывается в сигнале.

   Эти полуинтуитивные соображения подтверждаются строгим анализом. В Приложении 4

приводится программа расчета спектральной функции гармонического сигнала с ограниченным число периодов. Приводятся также соответствующие графики спектральных функций для сигнала с разным числом периодов. Они демонстрируют, как формируется "пик" спектральной функции при увеличении числа периодов, и как, соответственно, растет разрешающая способность анализа.

   Приведенный  перечень, разумеется,  не исчерпывает всего многообразия модельных сигналов.  Правильный выбор модели сигнала зависит от многих факторов, которые определяются дополнительно в ходе экспериментов.

ПРИЛОЖЕНИЕ 2

Листинг программы спектрального анализа прямоугольного импульса

1. Задаем параметры моделирования и формируем исходный сигнал в виде одиночного импульса. Функцией pulstran  можно превратить его в последовательность импульсов, но для дальнейших вычислений это не обязательно.

%задаются параметры сигнала Ts=0.01;     % период отсчетов T=10;          % длительность сигнала A=0.75;       % высота импульса tau=1;          % ширина импульса % строится входной сигнал t=-tau/2:Ts:T-tau/2; y=A*rectpuls(t, tau); figure(1); plot(t,y,'-'); grid % Наносятся обозначения title('input signal'); xlabel('time, s');

Рис.1. Исходный сигнал

1.  С помощью команды fft вычисляется прямое преобразование Фурье. Эта

команда возвращает вектор комплексных величин, включающий модуль и аргумент спектральной функции. Построим модуль спектра в соответствии  номеру элемента вектора:

% прямое преобразование Фурье x=fft(y); a=abs(x); figure(2) stem(a); grid title('fourier'); xlabel('element number');
	Рис.2. Результат работы быстрого преобразования Фурье

   Видно, что быстрое преобразование Фурье дает необычный способ размещения элементов спектрограммы, далее мы исправим это с помощью функции fftshift.

2.  Получение амплитудного спектра в привычной форме (для положительных и отрицательных частот)