Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 13

   По теореме Винера – Хинчина можно вычислить  взаимную  спектральную  плотность  этих процессов . Как показано в [ 6 ],  = , где  – комплексно сопряженная функция .

   Если система имеет комплексный коэффициент передачи , то справедливо очевидное равенство:  = , откуда следует

                            = =

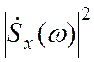
   Отсюда следует, что комплексный коэффициент передачи системы равен отношению взаимного спектра выходного и входного сигналов к энергетическому спектру сигнала. В пакете МАТЛАБ есть готовые процедуры для оценки по спектрам мощности входного и выходного сигналов и их взаимной спектральной плотности. Необходимо только, чтобы входной и выходной сигнал задавались реализациями с одинаковым числом отсчетов .

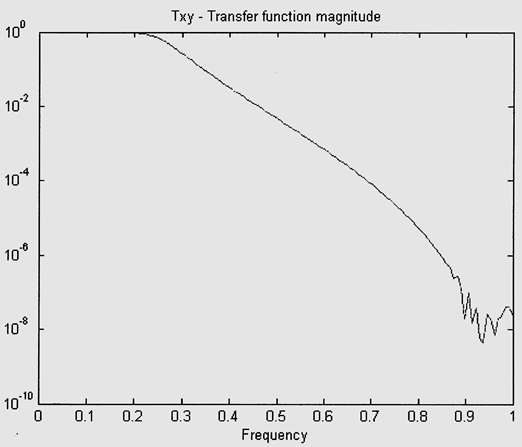
   В качестве примера покажем результат применения такой процедуры для оценки модуля коэффициента передачи простейшей линейной цепи – интегрирующей цепочки. Он показан на Рис.5.5, вертикальный масштаб – логарифмический (в децибелах):

 

Рис.5.5. Модуль коэффициента передачи интегрирующей цепочки

Видно, что частотная характеристика испытывает монотонный спад в области высоких частот, что соответствует назначению этой цепочки. Флуктуации в нижней правой части рисунка – из за нарушения точности вычислений при работе с малыми величинами.

   Весь материал, изложенный выше, касался только стационарных случайных процессов. На практике, многие нестационарные процессы можно исследовать,  если их разбить на ряд интервалов на каждом из которых процесс можно считать локально стационарным. Такой подход широко применяется в  исследованиях, но в наших экспериментах  мы ограничимся только стационарными процессами.

Раздел 6. ЗАДАНИЯ К РАБОТЕ

   В практической части работы необходимо будет выполнить ряд заданий по расчету спектральных характеристик модельных детерминированных сигналов, а также проанализировать спектры экспериментально зарегистрированных детерминированных и случайных сигналов.

   Математический пакет МАТЛАБ содержит ряд функций для спектрального анализа как детерминированных, так и случайных сигналов. В качестве предварительного этапа к выполнению практической части работы необходимо ознакомиться с  ними. Эти функции рассчитаны на обработку цифровых (дискретных) сигналов. Начнем с  детерминированных  сигналов, для них  существуют специальные функции преобразования Фурье:

     FFT (Fast Fourier Transformation) – быстрое преобразование Фурье,

     IFFT (Inverse Fast Fourier Transformation) – быстрое обратное преобразование Фурье. .

    Весьма полезной для правильного представления результатов анализа является также функция FFTSIFT – функция перегруппировки выходного массива преобразования Фурье.

    Кратко рассмотрим перечисленные функции. Если исходный аналоговый сигнал u(t) преобразован в цифровой сигнал x (представляющий собой вектор с конечным числом элементов n) , то

y=fft(x,n) – прямое дискретное преобразование Фурье,   его результат:

 

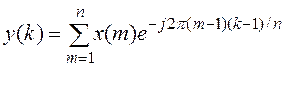                                                                                                                                                                                                  (6.1)

    Обратное преобразование Фурье :x=ifft(y,n)  даст исходный вектор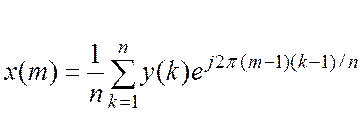        

(6.2)

n – число элементов заданного вектора x (оно является также размером выходного вектора y). Номер m соответствует моменту времени t_m , в который измерен входной сигнал x(m); при этом t₁=0. Номер k – это индекс значения частоты f_k , которому соответствует найденный элемент y(k) дискретного преобразования Фурье.

   Быстрое преобразование Фурье – особый вычислительный прием, убыстряющий расчеты по ф-лам (6.1) и (6.2). Подробнее с этим алгоритмом можно ознакомиться в  [ 6, 7 ]. Однако, результаты его применения дают непривычный порядок расположения спектральных компонент. Для приведения его к обычному виду, при котором нуль частоты располагается в середине шкалы частот, применяется функция FFTSIFT (например, она применена при построении спектрограммы Рис.2.3.).