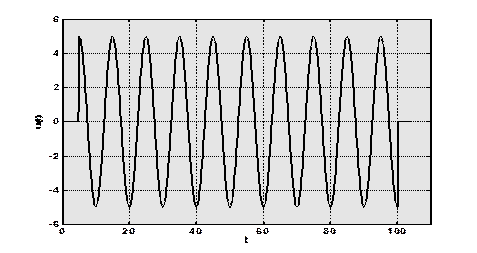
Рис.1.1. Гармонический сигнал конечной длительности
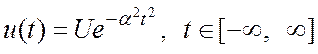 (1.2)
(1.2)
Вид этого сигнала представлен на Рис.1.2:
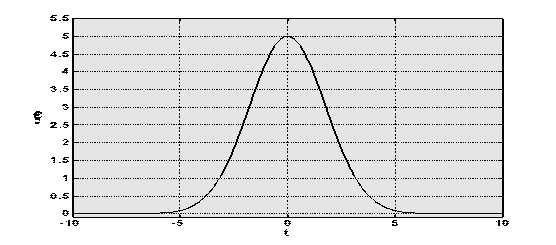
Рис.1.2. Гауссов импульс.
· непрерывный сигнал (экспоненциальный импульс)
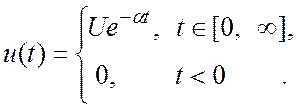 (1.3)
(1.3)
Этот сигнал представлен на Рис.1.3
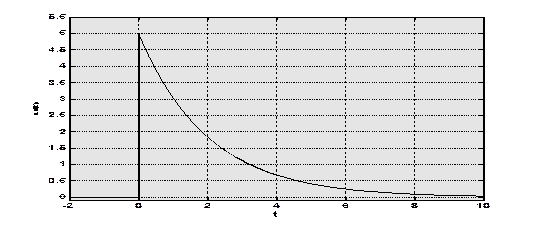
Рис.1.3. Экспоненциальный импульс
·
финитный сигнал, т.е. принимающий отличные от нуля значения на ограниченном
интервале времени ![]() (прямоугольный видеоимпульс):
(прямоугольный видеоимпульс):
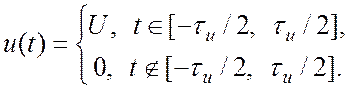 (1.4)
(1.4)
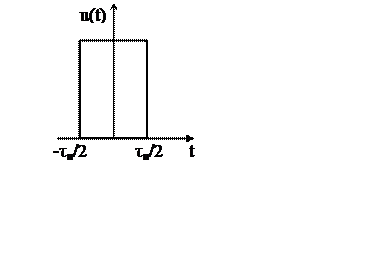
Рис. 1.4. Прямоугольный видеоимпульс
Заметим, что термин "видео" в этом контексте совсем не подразумевает отношения сигнала к телевизионной технике. Смысл термина выяснится в ходе дальнейшего изложения.
· Ещё один финитный сигнал - треугольный видеоимпульс
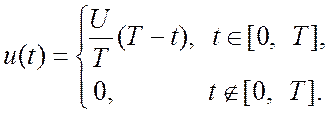 (1.5)
(1.5)
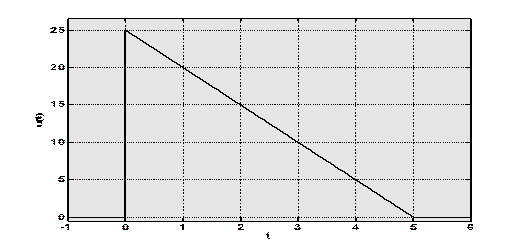
Рис. 1.5. Треугольный видеоимпульс
· функция Дирихле:
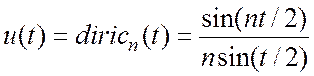 (1.6)
(1.6)
эта функция имеет равномерный спектр
в полосе частот от нуля до ![]() , её график показан на
Рис.1.6.
, её график показан на
Рис.1.6.
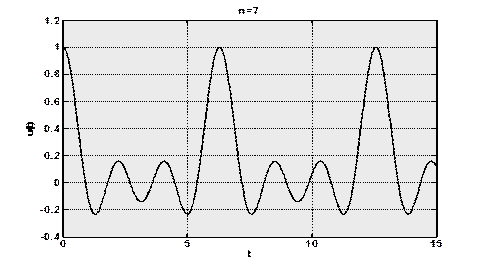
Рис.1.6. Функция Дирихле
Разумеется, приведенный перечень не исчерпывает всего многообразия модельных сигналов. Правильный выбор модели в общем случае зависит от искусства экспериментатора.
Тестовые сигналы. Особое место среди математических моделей сигналов занимают модели тестовых сигналов, т.е. испытательных или пробных. Они широко используются в теоретических исследованиях, а приближенно отвечающие им физические (радиотехнические) сигналы – в экспериментальной практике физического эксперимента.
Одним из наиболее известных тестовых сигналов является единичная ступенчатая функция, функция включения, или функция Хевисайда:
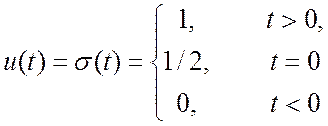 (1.8)
(1.8)
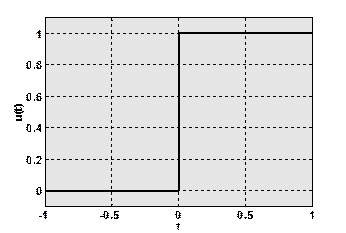
Рис.1.7. Функция Хевисайда
Важнейшим тестовым сигналом является также дельта-функция, или функция Дирака.
Она определяется соотношениями:
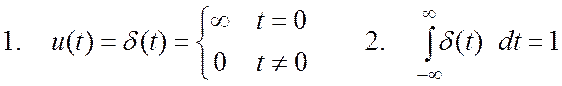 (площадь δ-функции) (1.9)
(площадь δ-функции) (1.9)
Из первой части определения (1.9) следует, что δ(t) существует лишь при нулевом значении аргумента, поэтому справедливо:
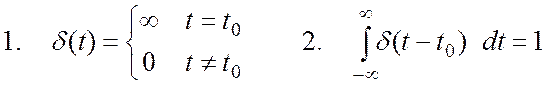 (1.10)
(1.10)
Из второй части определения следует, что размерность δ(t) обратна размерности аргумента t. Отметим также важное соотношение, определяющее так называемое фильтрующее свойство δ-функции:
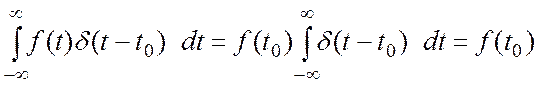 (1.11)
(1.11)
т, е. определенный интеграл, подынтегральная функция которого содержит в качестве сомножителя δ-функцию, равен значению этой функции с аргументом, при котором
δ -функция равна нулю. Это свойство легко доказывается с использованием теоремы о среднем.
Дельта – функция - это математическая функция. Её физическую модель можно задать следующим образом. Пусть имеется прямоугольный импульс вида (1.4), длительность которого равна tи , а амплитуда равна 1/ tи (Рис. 1.8). Если последовательно стремить tи к нулю, то высота импульса устремится к бесконечности, а площадь импульса остается равной единице, что и требуется от дельта – функции.

Рис.1.8. Иллюстрация к определению δ –функции.
Функция δ(t) относится к так называемым обобщенным, символическим функциям. С ее помощью, например, определяют не существующую в классическом смысле производную функции Хевисайда:
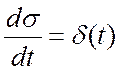 (1.12)
(1.12)
В свою очередь, функция Хевисайда (1.8) может быть на основании (1.12) определена так
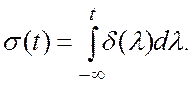 (1.13)
(1.13)
Кроме указанных функций, тестовой является гармоническая функция включения:
![]()
![]()
которую, используя функцию Хевисайда, можно записать как ![]()
Этот сигнал показан на Рис.1.9.
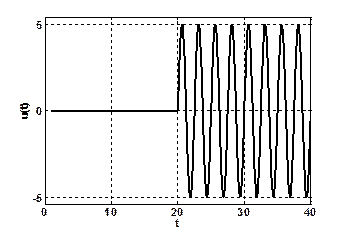
Рис. 1.9. Гармоническая функция включения.
Радиосигнал. Так называют сигнал, модель которого представляется в форме:
![]() (1.14)
(1.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.