Соответствующая
кривая изображена сплошной линией на Рис.11.7 в плоскости ![]() . Геометрическое место точек поворота в
этой плоскости является эллипсом
. Геометрическое место точек поворота в
этой плоскости является эллипсом
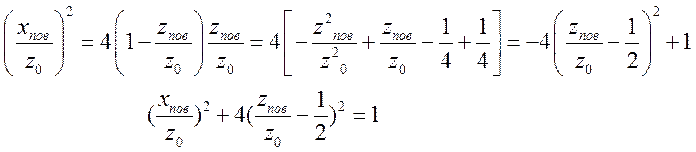 .
.
Определим
положение каустики в плоскости ![]() из системы уравнений
из системы уравнений
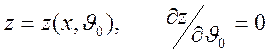 ,
,
которая приводится к виду
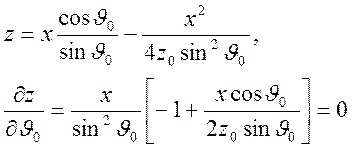 .
.
Исключая
угол ![]() из этой системы, получим уравнение
каустики
из этой системы, получим уравнение
каустики
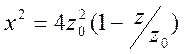 .
.
Линия
каустики в плоскости ![]() является параболой с вершиной
при
является параболой с вершиной
при ![]() . Она изображена штриховой линией на
Рис.11.7, 11.8 и 11.9. На Рис.11.8 показана качественная картина семейства
лучей для линейного профиля неоднородности среды. Каустика в этом случае
разделяет пространство на область «тени» (в ней нет лучей) и «освещенную»
область, в которой в каждую точку приходят от источника два луча. На Рис.11.9
сплошными линиями показано семейство поверхностей равной фазы. «Яйцеобразный»
вид фазовых поверхностей в начальные моменты времени, (пока лучи еще не
достигли каустики), связан с тем, что фазовая скорость волны в направлении
возрастания
. Она изображена штриховой линией на
Рис.11.7, 11.8 и 11.9. На Рис.11.8 показана качественная картина семейства
лучей для линейного профиля неоднородности среды. Каустика в этом случае
разделяет пространство на область «тени» (в ней нет лучей) и «освещенную»
область, в которой в каждую точку приходят от источника два луча. На Рис.11.9
сплошными линиями показано семейство поверхностей равной фазы. «Яйцеобразный»
вид фазовых поверхностей в начальные моменты времени, (пока лучи еще не
достигли каустики), связан с тем, что фазовая скорость волны в направлении
возрастания ![]() оказывается больше, чем в противоположном
направлении.
оказывается больше, чем в противоположном
направлении.
2).
В случае полу бесконечного линейного слоя в области ![]() ,
граничащего с однородным полу пространством
,
граничащего с однородным полу пространством ![]() (Рис.11.10).
Функция
(Рис.11.10).
Функция ![]() имеет вид
имеет вид
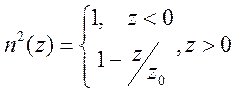 .
.
Форма
каустики усложняется. Вместо гладкой формы, теперь возможно появление каустик с
особенностями в виде «петли» с двумя точками заострения («ласточкин хвост»).
Форма каустики при этом зависит от положения точечного источника (![]() ). В области
). В области ![]() среда
однородная и лучи здесь представляют собой прямые линии. В области
среда
однородная и лучи здесь представляют собой прямые линии. В области ![]() профиль неоднородности линейный и лучи
здесь имеют вид отрезков парабол. Не приводя формул для описания
геометрического места точек поворота и каустики, отметим основные
закономерности лучевой картины. Оказывается, что каустика имеет гладкую форму,
если источник расположен либо ниже уровня
профиль неоднородности линейный и лучи
здесь имеют вид отрезков парабол. Не приводя формул для описания
геометрического места точек поворота и каустики, отметим основные
закономерности лучевой картины. Оказывается, что каустика имеет гладкую форму,
если источник расположен либо ниже уровня 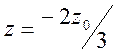 , либо
выше уровня
, либо
выше уровня 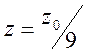 . При условии
. При условии 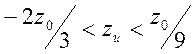 на
каустике имеются точки заострения, ограничивающие каустическую петлю. Эволюция
формы каустики при изменении высоты положения источника показана на Рис.11.11.
При
на
каустике имеются точки заострения, ограничивающие каустическую петлю. Эволюция
формы каустики при изменении высоты положения источника показана на Рис.11.11.
При 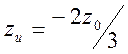 и
и 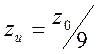 петля
на каустике стягивается в каустические фокусы
петля
на каустике стягивается в каустические фокусы ![]() и
и
![]() . Через каждую точку внутри каустической
петли проходит четыре различных луча. (три луча, претерпевших поворот и один
луч - прямой). Поясним появление петлеобразной каустики. Рассмотрим форму
линии, изображающей геометрическое место точек поворота лучей. При условии
. Через каждую точку внутри каустической
петли проходит четыре различных луча. (три луча, претерпевших поворот и один
луч - прямой). Поясним появление петлеобразной каустики. Рассмотрим форму
линии, изображающей геометрическое место точек поворота лучей. При условии 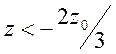 или
или 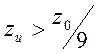 (такая
ситуация на Рис.11.12 и 11.13 отмечена буквой
(такая
ситуация на Рис.11.12 и 11.13 отмечена буквой ![]() ) линия
геометрического места точек поворота в плоскости
) линия
геометрического места точек поворота в плоскости ![]() является
монотонной (Рис.11.12). Монотонной при этом оказывается и линия каустики,
которая разделяет в этом случае пространство на область тени и на освещенную
область (в каждую точку здесь приходят два луча). В этом случае однозначной
будет зависимость дальности
является
монотонной (Рис.11.12). Монотонной при этом оказывается и линия каустики,
которая разделяет в этом случае пространство на область тени и на освещенную
область (в каждую точку здесь приходят два луча). В этом случае однозначной
будет зависимость дальности ![]() от угла выхода
от угла выхода ![]() (случай
(случай ![]() на
Рис.11.13). Ситуация изменяется при
на
Рис.11.13). Ситуация изменяется при 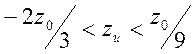 (случай
(случай ![]() ). Как видно из Рис.11.13, некоторым
дальностям соответствуют три значения угла выхода
). Как видно из Рис.11.13, некоторым
дальностям соответствуют три значения угла выхода ![]() . В
соответствующую область пространства (в каустическую петлю приходят три луча,
претерпевших поворот). В случае
. В
соответствующую область пространства (в каустическую петлю приходят три луча,
претерпевших поворот). В случае ![]() геометрическое место
точек поворота лучей уже не является монотонной кривой (Рис.11.14). Не
монотонность этой кривой определяет особый характер каустики в случае
геометрическое место
точек поворота лучей уже не является монотонной кривой (Рис.11.14). Не
монотонность этой кривой определяет особый характер каустики в случае ![]() . Еще более сложный вид каустик может
возникать при рассмотрении лучевой картины для сред с другой зависимостью
показателя преломления от
. Еще более сложный вид каустик может
возникать при рассмотрении лучевой картины для сред с другой зависимостью
показателя преломления от ![]() . Естественно, что
картина лучей и конфигурация каустики еще более усложнится в случае, когда показатель
преломления зависит от всех трех координат
. Естественно, что
картина лучей и конфигурация каустики еще более усложнится в случае, когда показатель
преломления зависит от всех трех координат ![]() .
Дополнительное усложнение картины происходит в неоднородных анизотропных
средах.
.
Дополнительное усложнение картины происходит в неоднородных анизотропных
средах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.