Introduction to Quantum Electrodynamics, страница 8

                 Charge renormalization

The physical electron charge can be defined in the following way:

Let us consider two classical 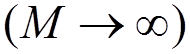 charged particles being at the rest at a large distance from each other  :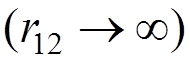

                                                         

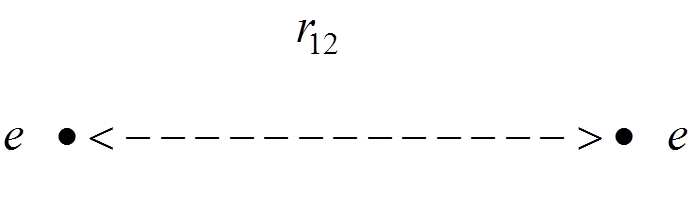
The interaction of  the charges is described by the Coulomb low

                                     ,

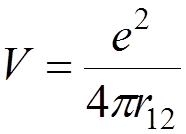where  is the physical  charge.

From the other side, the calculation within QED shows that, to the two lowest orders in  , the interaction is described by the diagrams

             

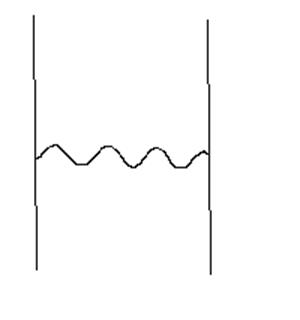
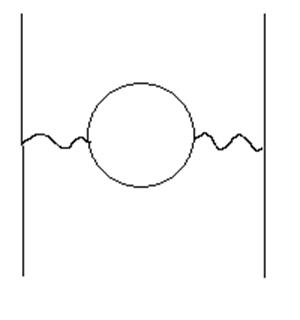
Their calculation yields

                        ,

where  is the regularization parameter for the one-photon-loop diagram. Comparing both formulas, we obtain

                     .

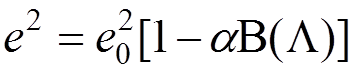It yields

                   ,

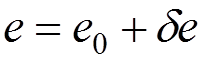where

                  .

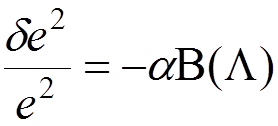Therefore, in our equations we should put

                   

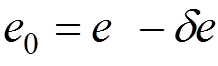
that is known as the charge renormalization.

In particular, the charge renormalization makes the vacuum polarization (VP) contribution to the energy shift of  an atomic level to be finite:

 

                                                            Interaction with 

                                                            the Coulomb field

                                                            of the nucleus

 

For low-Z H-like atoms, the VP energy shift is

                  

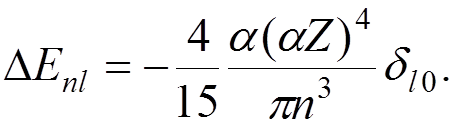
For the 2s state in hydrogen:

                  .

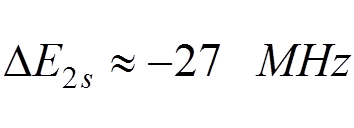References

[1]  J.J. Sakurai, Advanced Quantum Mechanics, 1967.

[2] V.G. Serbo and I.B. Khriplovich, Lectures on Quantum Mechanics,  (Novosibirsk State University, 1999).

[3] J.D. Bjorken and S.D. Drell, Relativistic Quantum Mechanics, 1964.

[4] V.B. Berestetskii, E.M. Lifshitz, and  L.P. Pitaevskii,

Relativistic Quantum Theory, 1971.

[5] W. Greiner, Quantum Mechanics. Special Chapters,

1998.

[6] W. Greiner and J. Reinhardt, Quantum Electrodynamics, 1992.

                          Appendix I

We consider  aspace of  functions

      

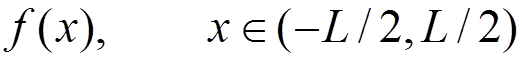
with the boundary conditions

              

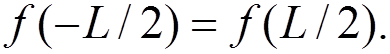
In this space, the momentum operator

                      

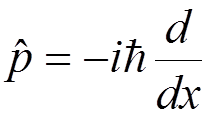
is Hermitian and has eigenfunctions

                     

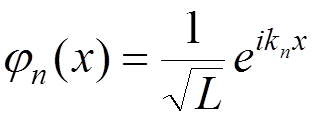
where 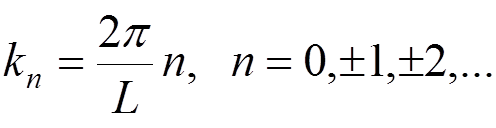 . The corresponding eigenvalues are 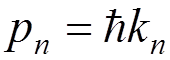.  For any  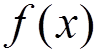 from the space under consideration we have      

If 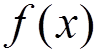 is real, we obtain

          

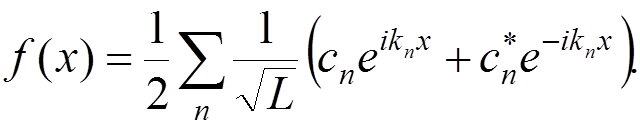
This expansion corresponds to the Fourier expansion in terms of  the “cos” and “sin” functions:

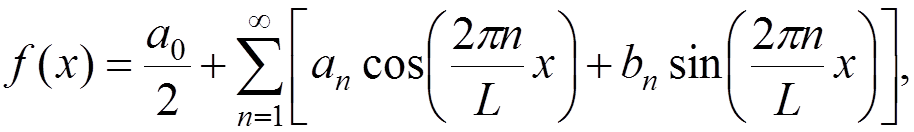
where

           

           

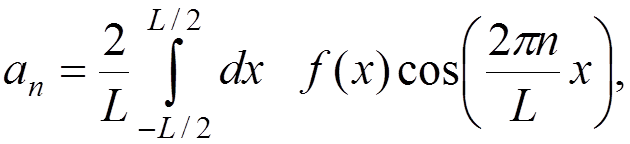
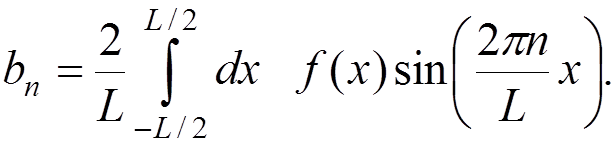
For an even function,  and, for an odd function, .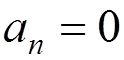 

The boundary condition 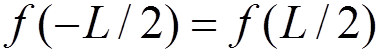 does not mean that  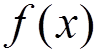is an even function.

                           Appendix II

Let us summarize the mass renormalization procedure

in the non-relativistic case. We start with the Schroedinger equation:

       

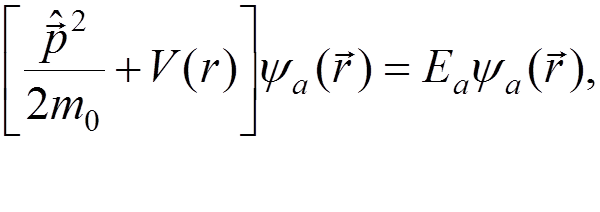
where   is the momentum operator and 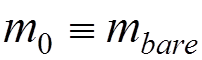 is the bare electron mass. Calculating the energy shift of the level “a” due to interaction with the quantized electromagnetic field, we get

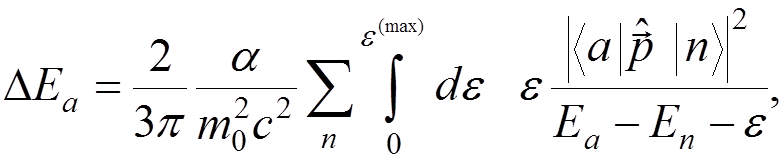
where . From the other side, the interaction

with the quantized electromagnetic field shifts the electron mass by

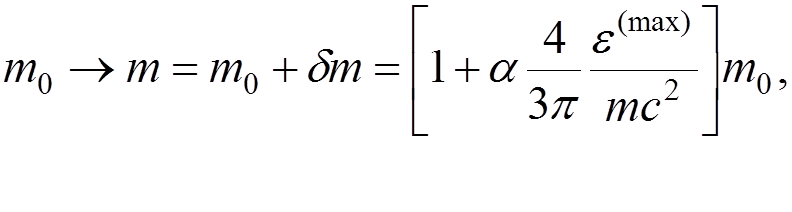
where  is the observable electron mass. Because we know from experiment only ,  we must express all physical quantities in terms of  but not  . With this in mind we should  put in the Schroedinger equation

                            

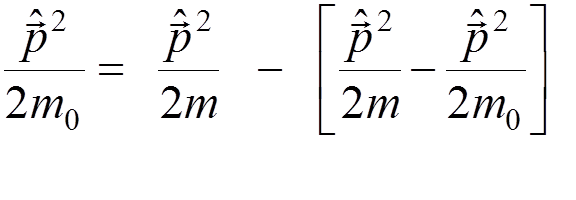
and consider the second term (which is ) by perturbation theory.

The observable energy shift is

.

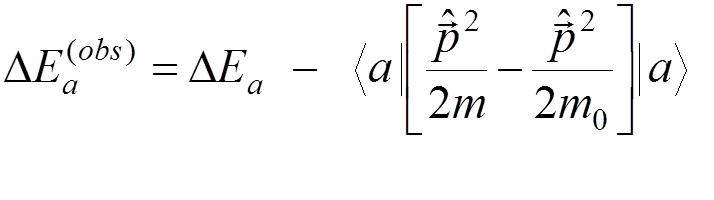
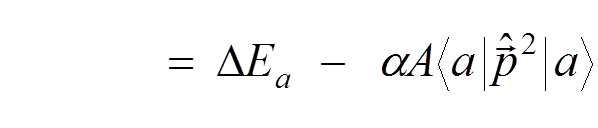Where in      we also  can use  instead of , because this replacement does not affect the energy shift

in order .