Introduction to Quantum Electrodynamics, страница 7

                                                                                                

This diagram is convergent.

                    One-loop divergent diagrams

________________________________________________

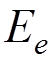
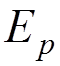                               Diagram                 Effective degree

 

 0             2                                        2              0

 

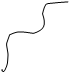 0             3                                       =0       Furry’s theorem

 

0              4                                         0              finite

 

 

2              0                                         1                  0

 

2              1                                         0                  0

Therefore, we have only the following one-loop divergent                                             diagrams: 

                                            

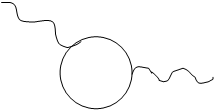
     Self energy                      Vacuum polarization                   

 

             

                                                            Vertex   

We regularize the corresponding integrals by a parameter   . They diverge as  .

                      Renormalization

Calculations by perturbation theory give all physical quantities (e.g., , , …)  in terms of the bare electron mass , the bare electron charge , and the regularization parameter  (  and  determine the electron mass and charge, if the interaction is switched off):

                  .

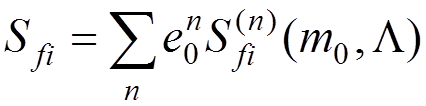When the interaction is switched on,   and   are not more  physical quantities.  The observed (physical) electron mass and charge can be calculated by perturbation theory

                  ,

                  .

The physical values of  and  are known from experiment. Using the smallness of , we can invert the equations for   and :

                  ,

                  .

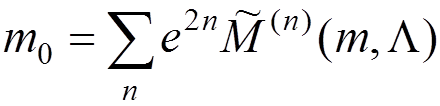Substituting these expressions for   and  into the equation for , we obtain

                    .

It can be shown that   is finite (in every order in ) as

 .

                        Mass renormalization

Let us consider the self-energy  (SE) diagram for a free electron

                                           

A direct evaluation of this diagram yields

                       .

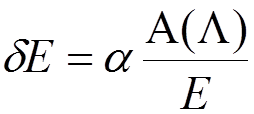From the other side,

 ,

because  is not changed due to this interaction. We have

                       .

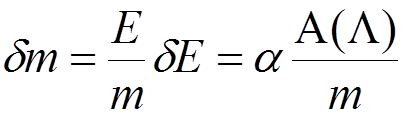So, the self-energy diagram changes the electron mass

               .

In the free-electron theory, this effect can be simply  accounted for by replacing  , where  is the physical electron mass, and by omitting the self-energy diagram. However, if the electron  is not free, the SE diagram has further effects. To account this effect in calculations of other physical quantities, we should put in our equations

                               .

It results in occurring the term

                    

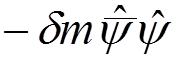
in the interaction Hamiltonian and  an additional vertex in the Feynman rules:

                                                                                                                                                                                                    

 

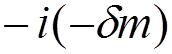
                 SE                                   mass counterterm

The calculation of the SE diagrams for a bound electron together with the counterterm results in the Lamb shift of atomic levels.