то функцию f(x) можно записать по формуле Тейлора
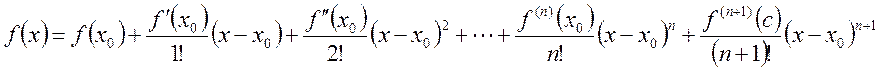 (14.6)
(14.6)
при ![]() , или по формуле Макларена
, или по формуле Макларена
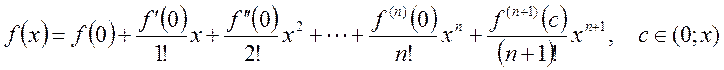 (14.7)
(14.7)
Разложение в ряд Макларена основных элементарных функций
1.
![]() . Используем
формулу (14.3). Так как
. Используем
формулу (14.3). Так как
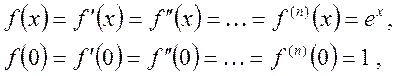
то по формуле (14.3) имеем
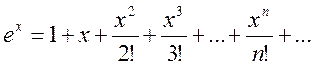 .
(14.8)
.
(14.8)
Находим радиус сходимости.
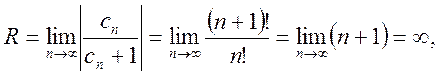
т.е. область сходимости ряда (14.8) ![]() .
.
2. f(x) = sin x. Вычислим производные и их значения в нуле
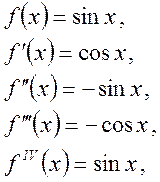
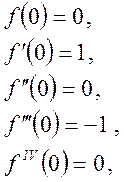
… … … … … … … … .
Очевидно, что производные четного порядка ![]() , а нечетного
порядка
, а нечетного
порядка ![]() , i= 1, 2, … . По формуле
(14.7)
, i= 1, 2, … . По формуле
(14.7)
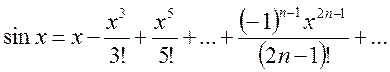 . (14.9)
. (14.9)
Область сходимости ![]()
3. f(x)= cos x. Аналогично получаем
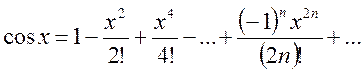 . (14.10)
. (14.10)
Область сходимости ![]() .
.
4.
![]() , где
, где ![]() . Вычислим производные и их значения в нуле
. Вычислим производные и их значения в нуле
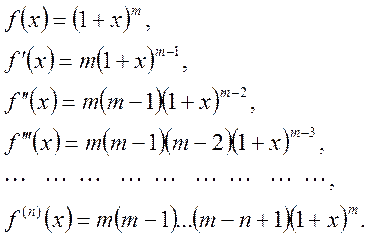
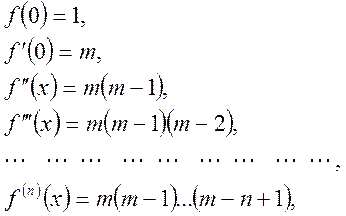
По формуле (14.3) находим
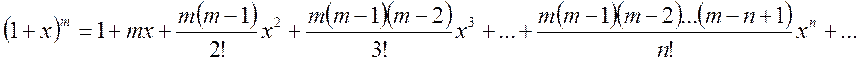 .(14.11)
.(14.11)
Интервал сходимости ряда (-1; 1) (на концах интервала при ![]() сходимость ряда
зависит от конкретных значений m.
сходимость ряда
зависит от конкретных значений m.
5. f(x)=ln(1+x)
Известно, что сумма бесконечно убывающей геометрической
прогрессии с первым членом ![]() и знаменателем q=x при |x|<1 вычисляется по формуле
и знаменателем q=x при |x|<1 вычисляется по формуле
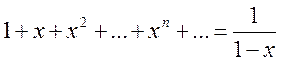 (14.12)
(14.12)
На последнее равенство можно смотреть как на разложение
функции 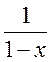 в степенной
ряд.
в степенной
ряд.
Полагая в равенстве (14.12) ![]() , получаем
, получаем
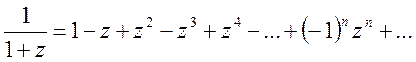 (14.13)
(14.13)
Интегрируя почленно равенство (14.13) в интервале (0; х), где |x|<1, получаем
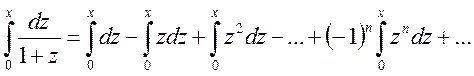
Отсюда
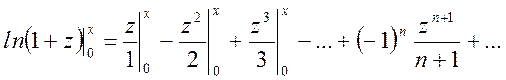
или
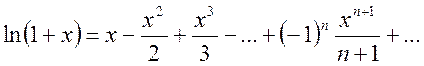 (14.14)
(14.14)
Область сходимости ![]() .
.
6.
![]() . Положим в
разложении (14.12)
. Положим в
разложении (14.12) ![]() , получим
, получим
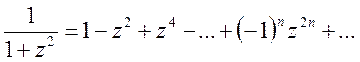 .
.
Интегрируя последнее равенство в пределах от 0 до х , где ![]() , получаем
, получаем
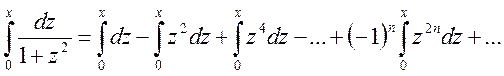 ,
,
или
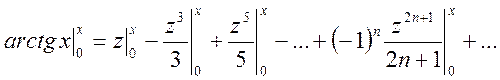
Так как arctg 0=0, то окончательно имеем
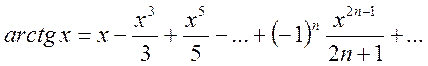 ,
(14.15)
,
(14.15)
Область сходимости ![]() . В частности,
при х=1 получаем
. В частности,
при х=1 получаем
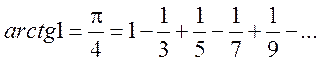
14.2. Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, приближенно вычисляют некоторые “неберущиеся” определенные интегралы, интегрируются дифференциальные уравнения. Приведем примеры.
Пример 1. Вычислить sin 1. Пологая в разложении (14.9) х=1, получаем
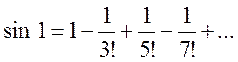
Если отбросить все члены, начиная с 4-го, то погрешность
будет по абсолютной величине меньше 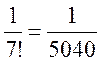 (так как ряд для
sin
1 есть ряд знакочередующийся). Отсюда
(так как ряд для
sin
1 есть ряд знакочередующийся). Отсюда 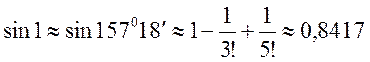 с точностью до
0,0002.
с точностью до
0,0002.
Пример 2. Вычислить ![]() .
.
Преобразуем это выражение 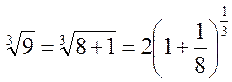 . Используем
разложение (14.11), полагая
. Используем
разложение (14.11), полагая 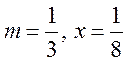 ;
;
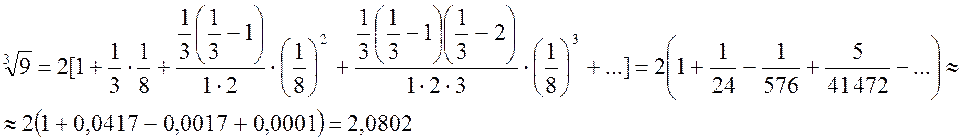
По таблицам ![]() =2,0801.
=2,0801.
Пример 3. Вычислить “не берущийся ” интеграл 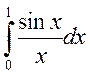 .
.
Решение. Разделив почленно ряд (14.9) на х, получим
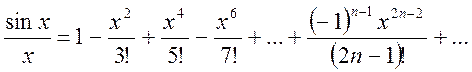 .
.
Отсюда, интегрируя почленно, получим
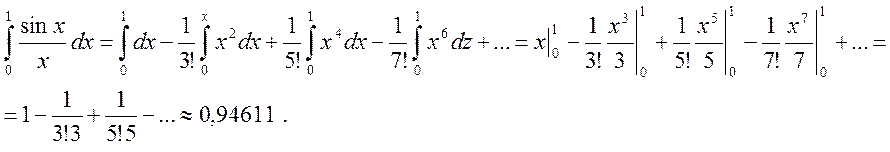
Так как ряд знакопеременный и модули его членов монотонно
убывают, то ограничившись тремя членами, получаем, что погрешность меньше 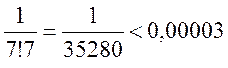 .
.
Пример 4. Найти 3 отличных от нуля члена разложения решения
дифференциального уравнения ![]() в степенной ряд.
в степенной ряд.
Решение. Решение дифференциального уравнения ищем в виде степенного ряда
![]() .
(*)
.
(*)
Подставляя начальные условия, находим 1=![]() .
.
Подставляем разложение (*)в исходное уравнение, вычисляя предварительно
![]() ,
,
получаем,
![]() .
.
Приравнивая коэффициенты при одинаковых степенях х в левой и правой части последнего равенства получаем систему уравнений для отыскания неизвестных коэффициентов разложения
![]()
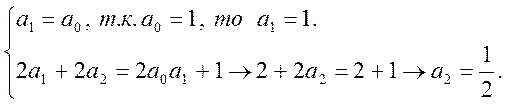
Тогда искомые три члена разложения решения уравнения в
степенной ряд запишутся 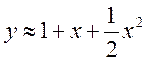 .
.
У П Р А Ж Н Е Н И Я
1. Разложить в степенной ряд по степеням х функции:
а)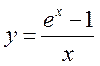 ; б)
; б)![]() ; в)
; в)![]() ;
;
г)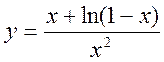 ; д)
; д)![]() е)
е)![]() .
.
2. Вычислить приближено с точностью до 0,0001:
а)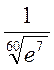 б)
б)![]() в)
в)![]() ;
;
г)![]() е)
е)![]() .
.
3. Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности:
а)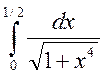 ; б)
; б)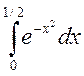 ; в)
; в)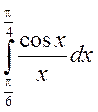 .
.
4. Найти три первых (отличных от нуля) членов разложения в степенной ряд решений данных уравнения при указанных начальных условиях:
а) ![]() б)
б)![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.