Следствие. Если n-ый член ряда при ![]() не стремится к
нулю, то этот ряд расходится.
не стремится к
нулю, то этот ряд расходится.
Доказательство. Предположим противное, т.е. ряд 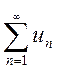 сходится. Но в этом случае из
приведенной выше теоремы следует, что
сходится. Но в этом случае из
приведенной выше теоремы следует, что ![]() ,
что противоречит условию, заданному в следствии, т.е. ряд
,
что противоречит условию, заданному в следствии, т.е. ряд 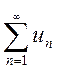 расходится.
расходится.
Пример 3. Исследовать сходимость ряда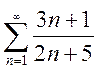 .
.
Решение. Проверяем выполнение необходимого условия сходимости.
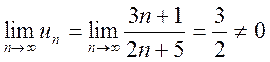 , т.е. необходимое условие сходимости не
выполняется, значит ряд расходится.
, т.е. необходимое условие сходимости не
выполняется, значит ряд расходится.
Замечание. Доказанный
необходимый признак сходимости ряда, вообще говоря, не является достаточным.
Можно привести примеры рядов, у которых ![]() (необходимое
условие выполнено), а ряд тем не менее расходится.
(необходимое
условие выполнено), а ряд тем не менее расходится.
Пример 4.Исследовать сходимость гармонического ряда
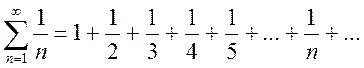 . (12,10)
. (12,10)
Решение. Проверим выполнение необходимого признака сходимости ряда:
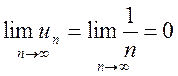 , он выполняется, но покажем, что
тем не менее ряд (12.10) расходится. Для доказательства расходимости построим
вспомогательное неравенство. Для этого запишем частные суммы
, он выполняется, но покажем, что
тем не менее ряд (12.10) расходится. Для доказательства расходимости построим
вспомогательное неравенство. Для этого запишем частные суммы ![]() и
и ![]() и
построим разность
и
построим разность ![]()
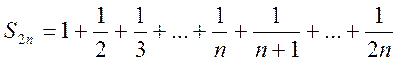 ,
,
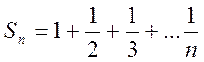 ,
,
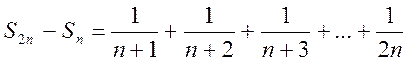 .
.
Заменяя в правой части
последнего равенства каждое слагаемое наименьшим из них, равным ![]() , получим вспомогательное
неравенство
, получим вспомогательное
неравенство
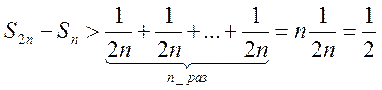 , т.е.,
, т.е., 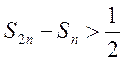 .
.
Предположим противное,
т.е. что гармонический ряд сходится, тогда ![]() .
Переходя к пределу в неравенстве, получим
.
Переходя к пределу в неравенстве, получим 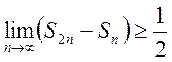 ,
или
,
или 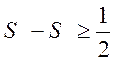 , или
, или 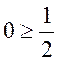 , т.е. получаем противоречие.
Значит, сделанное предположение о сходимости гармонического ряда неверно, т.е.
гармонический ряд расходится.
, т.е. получаем противоречие.
Значит, сделанное предположение о сходимости гармонического ряда неверно, т.е.
гармонический ряд расходится.
Таким образом, выполнение необходимого признака сходимости, вообще говоря, не дает возможности судить о сходимости данного ряда. Рассмотрим ниже достаточные признаки сходимости, которые позволяют в ряде случаев точно ответить на вопрос о сходимости или расходимости исследуемого ряда.
10.3. Достаточные признаки сходимости числовых рядов.
1. Первый признак сравнения.
Теорема. Пусть даны два
знакоположительных ряда 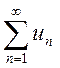 (1) и
(1) и 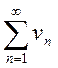 (2), причем члены первого ряда
не превосходят соответствующих членов второго ряда.
(2), причем члены первого ряда
не превосходят соответствующих членов второго ряда.
![]() . (12.11)
. (12.11)
Тогда: а) из сходимости ряда (2) следует сходимость ряда (1); б) из расходимости ряда (1) следует расходимость ряда (2).
Доказательство. а)
Пусть![]() и
и ![]() —
частичные суммы рядов (1) и (2), т.е.
—
частичные суммы рядов (1) и (2), т.е.
![]()
![]() .
.
Из неравенств (12.11)
следует, что ![]() . Так как ряд (2) сходится, то
существует конечный предел
. Так как ряд (2) сходится, то
существует конечный предел ![]() . Так как ряд
знакоположителен, то
. Так как ряд
знакоположителен, то ![]() и
и ![]() .
Таким образом, последовательность частичных сумм
.
Таким образом, последовательность частичных сумм ![]() монотонно
возрастающая (с ростом
монотонно
возрастающая (с ростом ![]() увеличивается сумма положительных
слагаемых) и ограничена (
увеличивается сумма положительных
слагаемых) и ограничена (![]() ). Следовательно, на основании
признака существования предела, последовательность
). Следовательно, на основании
признака существования предела, последовательность ![]() имеет предел, т.е. ряд (1)
сходится.
имеет предел, т.е. ряд (1)
сходится.
б)Применим метод доказательства от противного. Предположим, что ряд (2) сходится. Тогда согласно первой части теоремы (утверждение а)) ряд (1) тоже сходится, что противоречит предположению, т.е. ряд (2) расходится.
Замечание. Так как
сходимость ряда не изменится при отбрасывании конечного числа членов ряда, то
условие (12.11) не обязательно должно выполняться с первых членов рядов и
только для членов с одинаковыми номерами ![]() .
Достаточно чтобы оно выполнялось, начиная с некоторого номера
.
Достаточно чтобы оно выполнялось, начиная с некоторого номера ![]()
![]() , или чтобы
имело место неравенство
, или чтобы
имело место неравенство ![]() , где
, где ![]() .
.
Пример
5. Исследовать сходимость ряда 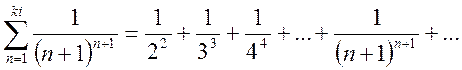
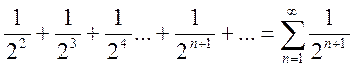 .
.
Это сходящийся
геометрический ряд при 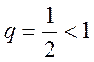 .
.
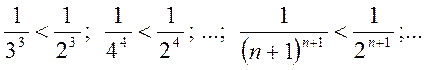
Тогда по первой теореме сравнения исследуемый ряд сходится.
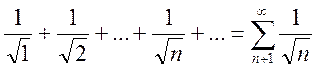 .
.
Решение.
Так как 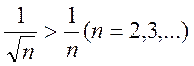 , то из сравнения с гармоническим
рядом (12.10), применяя первую теорему сравнения, делаем вывод, что исследуемый
ряд расходится.
, то из сравнения с гармоническим
рядом (12.10), применяя первую теорему сравнения, делаем вывод, что исследуемый
ряд расходится.
Очевидно, что при применении теоремы сравнения необходимо иметь набор так называемых “эталонных” рядов, используемых для сравнения. К таким рядам относятся:
1) геометрический
ряд 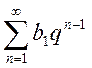 — сходится при
— сходится при ![]() , расходится при
, расходится при ![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.