есть ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин его членов  тоже сходится
(оба ряда геометрические со знаменателями, соответственно равными
тоже сходится
(оба ряда геометрические со знаменателями, соответственно равными ![]() и
и ![]() ).
).
Напротив, ряд
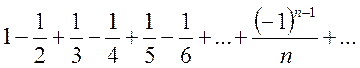 (13.5)
(13.5)
как мы увидим дальше, есть ряд сходящийся (см пр. 1), но он сходится условно, так как ряд, составленный из абсолютных значений его членов
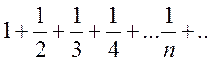 ,
,
расходится (гармонический ряд).
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают. Переставляя местами члены условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Под знакочередующимся рядом понимается ряд
![]() (13.6)
(13.6)
у которого любые рядом стоящие члены имеют противоположные знаки. Например, ряды (13.4) и (13.5).
Признак Лейбница.
Если в знакочередующемся ряде (13.6):
1) Члены ряда монотонно убывают по абсолютной величине
![]() ; (13.7)
; (13.7)
2)
Предел
общего члена ряда равен нулю при ![]() , т.е.
, т.е. ![]() .
.
Тогда:
I. знакочередующийся ряд сходится;
II.
его
сумма по абсолютной величине не превосходит первого члена ![]() ;
;
III. остаток ряда не превосходит по абсолютной величине первого отброшенного члена.
Доказательство. Рассмотрим частичные
суммы ряда (13.6) четных порядков ![]() и представим их в виде
и представим их в виде
![]() (13.8)
(13.8)
Так как
разности, стоящие в скобках в сумме (13.8), на основании условия (13.7)
неотрицательны, то последовательность частичных сумм ![]() , монотонно
возрастающая (с ростом
, монотонно
возрастающая (с ростом ![]() увеличивается число положительных слагаемых) и
ограниченная. Последнее можно увидеть, представив
увеличивается число положительных слагаемых) и
ограниченная. Последнее можно увидеть, представив ![]() в виде
в виде
![]() ,
,
откуда следует, что ![]() .
.
На основании
теоремы о существовании предела, последовательность ![]() имеет предел,
т.е
имеет предел,
т.е ![]() .
.
Рассмотрим
теперь последовательность частичных сумм нечетного числа членов при ![]() . Очевидно, что
. Очевидно, что
![]() .
.
причем по условию 2) ![]() . Тогда
. Тогда
![]() .
.
Итак, при любом ![]() (четном или
нечетном)
(четном или
нечетном) ![]() , т.е ряд сходится. Переходя к пределу в неравенстве
(13.9) получаем
, т.е ряд сходится. Переходя к пределу в неравенстве
(13.9) получаем ![]() . Остаток ряда (см. 12.5)
. Остаток ряда (см. 12.5)
![]()
представляет собой ряд, удовлетворяющий
условиям теоремы Лейбница, а это значит, что его сумма ![]() не превосходит
по модулю его первого члена, т.е
не превосходит
по модулю его первого члена, т.е ![]() . Таким образом, абсолютная
погрешность при замене суммы
. Таким образом, абсолютная
погрешность при замене суммы ![]() сходящегося знакопеременного ряда, удовлетворяющего
условиям теоремы Лейбница, частичной суммы
сходящегося знакопеременного ряда, удовлетворяющего
условиям теоремы Лейбница, частичной суммы ![]() его первых
его первых ![]() членов, не
превышает модуля первого отброшенного члена.
членов, не
превышает модуля первого отброшенного члена.
Пример 1. Исследовать
сходимость ряда ![]() .
.
Решение. Для этого ряда выполняются все условия теоремы Лейбница
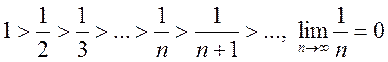
По теореме Лейбница ряд сходится.
Пример 2. Исследовать
сходимость ряда 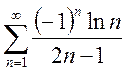 .
.
Решение. Проверим выполнение условий теоремы Лейбница, т.к. данный ряд знакочередующийся:
1)
 ,
,
2)
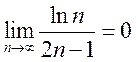 (Это можно доказать по правилу Лопиталя, считая
(Это можно доказать по правилу Лопиталя, считая ![]() независимой
переменной.)
независимой
переменной.)
Тогда исследуемый ряд сходится по теореме Лейбница.
Исследуем ряд на
абсолютную сходимость, исследуя ряд 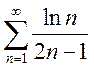 . Этот ряд расходится, так как
его члены больше членов расходящегося гармонического ряда, умноженного на
. Этот ряд расходится, так как
его члены больше членов расходящегося гармонического ряда, умноженного на ![]() :
: 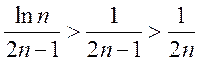 . Следовательно
данный ряд условно сходится.
. Следовательно
данный ряд условно сходится.
13.2 Функциональные ряды. Степенные ряды. Теорема Абеля.
Определение. Функциональным рядом называется ряд, члены которого являются функциями, т.е.
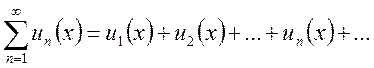 (13.10)
(13.10)
Отметим, что
изучение функциональных рядов сводится к изучению числовых. В самом деле, если ![]() , то для каждого
фиксированного значения аргумента
, то для каждого
фиксированного значения аргумента ![]() мы получаем соответствующий
числовой ряд
мы получаем соответствующий
числовой ряд
![]() ,
,
который или сходится или расходится.
Соответственно этому ![]() называется или точкой сходимости, или точкой
расходимости данного функционального ряда, совокупность всех точек
сходимости функционального ряда называется его областью сходимости.
называется или точкой сходимости, или точкой
расходимости данного функционального ряда, совокупность всех точек
сходимости функционального ряда называется его областью сходимости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.