ЭВМ в технике и научных исследованиях: Учебное пособие, страница 5

Таким образом, метод «крупных» частиц позволяет рассчитывать низкотемпературную плазму с учетом всевозможных физических эффектов. Как и в случае электронного потока, алгоритм реализует множество элементарных расчетов в малый промежуток времени.

Алгоритмы метода «частицы-в-ячейках» в литературе кодируются соотношением nDmV, где n – число пространственных координат, m – число учитываемых скоростей частиц.

2.8. Задачи оптимизации

Заданы многомерная функция , где –  n-мерный вектор, и ограничения , . Требуется найти глобальный экстремум функции , - глобальный экстремум, если для любого .

Функция называется целевой функцией, функции – функциями ограничения. Аргумент вектор называется планом, – оптимальным планом (или точкой глобального экстремума).

Если  и  – линейные функции (рис. 13), то задача относится к разделу линейного программирования.

Если  – нелинейная функция, то задача относится к нелинейному программированию. В случае нелинейного программирования функции 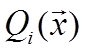могут отсутствовать.

В задачах линейного программирования экстремум находится на границе функции ограничения.

К нелинейному программированию приводят многие задачи, связанные с физическими моделями живого и неживого мира. Для решения задачи линейного программирования существует много эффективных пакетов. В отличие от них задачи нелинейного программирования являются проблемными, сложность увеличивается с увеличением размерности вектора  .

Нелинейные функции встречаются в реальных задачах и имеют не один, а много экстремумов. Задача может заключаться как в отыскании глобального максимального экстремума, так и глобального минимального экстремума. Эти задачи эквивалентны. Одна можно перевести в другую изменением знака функции.

Если дифференцируема, то необходимым условием экстремума является равенство 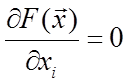, i =1, 2 , …, n.

Достаточное условие глобального экстремума  для любого .

Достаточное условие локального экстремума  для любого  из окрестности .

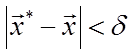Для отыскания локальных экстремумов существует множество численных методов. Одними из наиболее часто используемых методов являются градиентные методы.

В градиентном методе сначала выбирается начальная точка, от которой начинается оптимизация. Затем делаются шаги в направлении градиента:

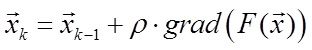                       , где                                   (25)

до тех пор, пока значение функции в очередной точке не станет меньше значения функции в предыдущей точке. Тогда значение ρ уменьшается, и итерации начинаются снова из предыдущей точки. Этот процесс повторяется, пока ρ не станет меньше заданной точности.

Для вычисления глобального экстpемума функции необходимы специальные методы локализации области глобального экстpемума и многокpатное пpименение метода поиска локального экстpемума. Одним из подходов поиска глобального экстpемума является динамическая пpоцедуpа – метод Монте-Каpло. Однако пpименение этой пpоцедуpы тpебует значительных вpеменных затpат. Для целенапpавленной локализации области глобального экстpемума можно пpедложить метод последовательного пpиближения pешения задачи, где на каждом шаге k+1 функция D_k+1 отpажает более точное пpиближение pешения задачи по отношению к функции D_k . Если на k-ом шаге вычислен вектоp , то можно пеpейти к более точному поиску экстpемума для более точной функции D_k+1 , если за начальный вектоp поиска D пpинять оптимальный план пpедыдущего шага. Схема такого поиска может быть отpажена в виде

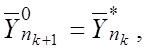
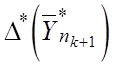                             ®                  .                 (26)

                                                          k=1,2,...

Пpи k=1  может быть положен пpоизвольным обpазом. Пpедполагается, что D_k  достаточно точно отpажает pешение задачи так, что D является pешением задачи тpебуемой точности. Такая последовательность оптимизационных шагов часто пpиводит к быстpому вычислению глобального экстpемума. Локализация области глобального экстpемума на каждом шаге достигается за счет вычисленного локального экстpемума на пpедыдущем шаге и поиска экстpемума на пеpвом шаге, если этот начальный поиск приводит к глобальному экстремуму для функции D₁ . Применительно к итерационным пpоцедуpам минимизации ошибки D различные точности описания могут быть получены за счет изменения количества узлов аппроксимации решения. Пусть Î R_n являются искомыми узлами аппроксимации решения задачи вычисления многомерного приближения. Уменьшая шаг h и увеличивая соответственно количество узлов N, можно построить аналогичную (26) пpоцедуpу минимизации ошибки приближения нелинейной целевой функции.

2.9. Распознавание образов  и обучение машин

Одним из наиболее интенсивно развивающихся  направлений применения ЭВМ в последнее время стали системы распознавания образов.

В общем виде задача распознавания образов состоит в следующем. Если некоторый объект в процессе своего функционирования однозначно описывается вектором признакового пространства , то представляет интерес определить при известном значении состояние объекта, представленное классом (образом) , s = 1, 2, …, p, где p – количество классов (образов).

Распознавание образа проводится с помощью разделяющей многомерной функции  такой, что каждому значению аргумента  ставится в соответствие класс , s – номер класса (образа).

Построение функции F осуществляется с помощью множества 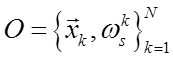, которое составляет обучающую матрицу, где N – количество известных образов.

Если задана некоторая модель функции F, то задаётся алгоритм определения (настройки) этой модели с помощью обучающего множества О. Если, таким образом, функция F определена, то далее для любого значения аргумента  возможно определение класса .

Задача распознавания образов имеет множество практических применений.

1.  Распознавание множества букв.

Для решения этой задачи  могут быть использованы разные множества признаков. Например, длина отрезка от соответствующей точки квадрата до границы буквы (рис. 14). У каждой буквы свои значения отрезков. Таким образом, класс соответствует определённой букве алфавита. Количество классов p соответствует количеству букв в алфавите. Очевидно, для каждой буквы вектор  принимает определённое значение, если для каждой буквы алфавита известно множество О, то далее для любого  множество может быть определено с помощью какого-либо алгоритма.