В случае решения задачи с
помощью кусочных функций появляется дополнительная задача – сшивание кусков ![]() . Существуют точный и приближенный
методы сшивания. При точном методе – «сшивание встык» – требуется обеспечить
непрерывность самой кусочной функции и непрерывность ее производных на некотором
дискретном множестве граничных точек.
. Существуют точный и приближенный
методы сшивания. При точном методе – «сшивание встык» – требуется обеспечить
непрерывность самой кусочной функции и непрерывность ее производных на некотором
дискретном множестве граничных точек.
Однако получающиеся при этом уравнения “сшивания” конечных элементов вместе с уравнениями, получаемыми при решении вариационной задачи, приводят к необходимости численного решения больших разреженных систем уравнений со сложным заполнением элементов матрицы. Для решения таких систем уравнений применяют специальные методы упорядочивания элементов матрицы. Таким образом, решение многомерных вариационных задач методом конечных элементов усложняется.
Во многих случаях
требуется обеспечить лишь достаточно хорошую непрерывность и гладкость кусочной
функции. Тогда применяется приближенный метод сшивания – «сшивание внахлест»
или «метод подвижного элемента», при котором минимизируются дефекты сшивания.
Решение требует минимизации двух ошибок: ошибки аппроксимации решения задачи ![]() и ошибки сшивания
и ошибки сшивания ![]() . Сшивание осуществляется следующим
образом: на середину одного куска накладывается один из углов другого куска
(рис. 8). Тогда ошибка сшивания в центре
. Сшивание осуществляется следующим
образом: на середину одного куска накладывается один из углов другого куска
(рис. 8). Тогда ошибка сшивания в центре ![]() будет
будет
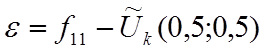 . Ошибка же аппроксимации
. Ошибка же аппроксимации 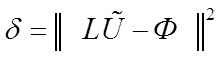 .
.
При решении задачи математической физики методом наименьших квадратов для одновременной минимизации ошибок сшивания и ошибки аппроксимации часто используется весовой метод. В этом методе минимизируется выражение:
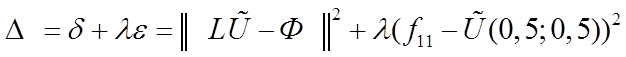 , (11)
, (11)
где λ - весовой коэффициент.
В случае решения уравнения Лапласа уравнение (11) приобретает вид:
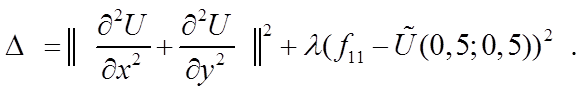 (12)
(12)
|
Рис. 8 |
Необходимым условием экстремума является
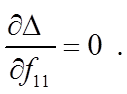 (13)
(13)
После подстановки в (13) выражения (12) и проведения преобразований, получается следующее соотношение для значений функции:
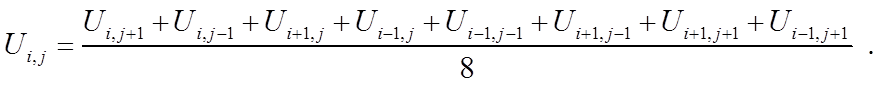 (14)
(14)
Последнее уравнение относится к вариационно-разностным. При использовании «сшивания внахлест» ошибка сшивания одинакова и для n-мерной задачи без увеличения сложности алгоритма сшивания.
При решении задач математической физики вариационным методом точность полученного решения выше, чем при использовании конечно-разностного метода.
2.5. Численное решение нестационарных задач
Значительная часть задач математической физики, например теплопередача и диффузия, относится к нестационарным задачам. Процесс распространения тепла в одномерном стержне описывается уравнением теплопроводности:
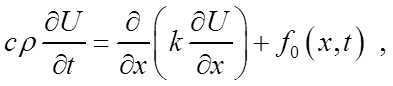 (15)
(15)
где U =U(x, t) – температура в точке x стержня в момент времени t;
r – линейная плотность;
c – удельная теплоемкость;
функция f0 – плотность тепловых источников;
k – коэффициент теплопроводности.
В общем случае c, r, k, f0 могут зависеть не только от x и t, но и от температуры Uи даже от производных ¶U/¶x.
Если k,c,r постоянны, то (15) можно записать в виде соотношения
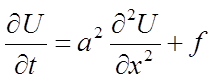
f=f0/(cr) (16)
a2=k/(cr) .
Соответствующая постоянная a называется коэффициентом температуропроводности. Таким образом, область D задачи математической физики, решение уравнения теплопроводности представляет собой, в нашем случае, прямоугольник координат (x, t)
Dо б л = {0£x£l, 0<t<T}.
Рассмотрим решение уравнения теплопроводности методом конечных разностей.
|
Рис. 9 |
Решение задачи методом конечных разностей будем искать в классе сеточных функций. Для этого построим сетку W с шагом h по координате x и с шагом t по времени (рис. 9). Через индексы i и j координата x для номера i будет равна произведению номера узла на шаг h. Соответственно по времени tj момент времени будет равен произведению слоя по времени jна временной шаг t.
Если число узлов равно N по координате x ,то шаг h будет равен отношению длины стержня к числу узлов по координате x и соответственно шаг t – отношению максимального временного момента рассмотрения по времени к числу временных слоев L.
W h , t={ (x i, t j):x i =ih, t j =jt,
h=l/N, где N-число узлов,
t=T/L
i=0,1,…N, j=0,…L}. (17)
Для аппроксимации необходимых нам частных производных, вторых частных производных по x и первых частных производных по t используем разделенные конечные разности первого порядка по t и второго порядка по x. Таким образом, индекс i является номером слоя по координате x, а индекс j является номером временного слоя. Разделенная конечная разность по времени имеет вид:
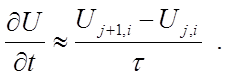
Заметим, что если для двух слоев j и j+1 временного слоя вычислить разделенную конечную разность, то этой разделенной конечной разности можно сопоставить частные производные по xj-го и (j+1)-го слоя. Таким образом, имеет место неоднозначность
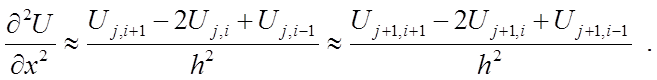 (18)
(18)
Для устранения этого противоречия вводится коэффициент b, с помощью которого усредняем слои j и j+1 временной слой с помощью линейного соотношения. В зависимости от параметра b, который очевидно меняется в пределах от 0 до 1, вес j-го или (j+1)-го слоя U можно регулировать.
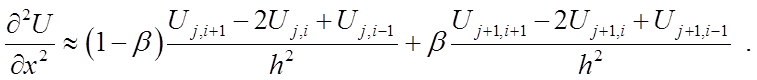
Рассмотрим различные схемы для различных значений b.
При b=0 имеет место соотношение
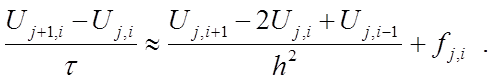 (19)
(19)
Физически мы распространяем вторую частную производную как на временной слой j, так и на временной слой j+1.
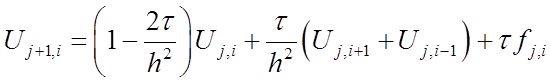 . (20)
. (20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.