Основы теории рентгенографических исследований. Физические принципы рентгеноструктурного анализа глобулярных белков (Разделы 1-2 учебного пособия "Рентгенография биологических объектов"), страница 6

                                        ,                                    (2.4)

 проведенный из узла с координатами (0, 0, 0). Если сравнить (2.3) и (2.4), то для ортогональных элементарных ячеек имеем

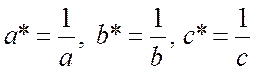                                       .                                 (2.5)

В результате соотношения

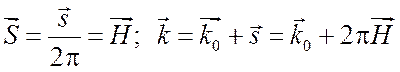                                                    (2.6)

являются условиями дифракции от кристалла. Из выражения (2.6) с учетом (1.6) можно получить формулу Брэггов-Вульфа (1.1). В дифрагированном излучении при определенном положении кристалла возникают только те пучки, которые соответствуют пересечению узла обратной решетки и сферы Эвальда (см. рис. 2.4). Поэтому от ориентации кристалла относительно первичного пучка и радиуса сферы отражения () зависит возникновение дифракционных пучков.

Связь между структурой кристалла с осевыми векторами  и его обратной решеткой, характеризующейся векторами , можно получить из скалярных произведений

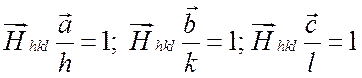                               ,                        (2.7)

которые получаются, если . Соотношения (2.7) называются условиями Лауэ.

Так как , то из условий Лауэ следует, что  а произведения, подобные , равны нулю. Таким образом, разноименные векторы кристаллической и обратной ей решетки взаимно-перпендикулярны. В общем случае связь между векторами  и  дается следующими соотношениями:

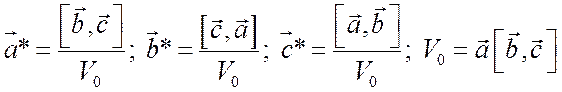                 ,         (2.8)

где  – объем элементарной ячейки кристалла, а квадратными скобками обозначено векторное произведение.

Как уже было сказано выше, векторы  характеризуют структуру кристаллической решетки. Векторы же  определяют положение проведенной через их концы плоскости кристаллической решетки , которая находится на расстоянии  от начала координат. С помощью трех целых чисел  которые называются миллеровскими индексами, можно задать все возможные кристаллические плоскости, «отражением» от которых образуются различные дифракционные пучки (рис. 2.5).

Рис. 2.5. Наборы отражающих плоскостей, характеризующиеся

различными индексами  (ортогональная решетка)

Из соотношений (2.7) путем попарного вычитания получаются три скалярных произведения

,

,

,

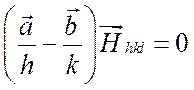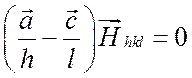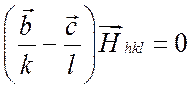которые позволяют заключить, что вектор  перпендикулярен к плоскости с индексами  и вообще всему набору или семейству параллельных друг другу плоскостей, которые проходят через концы векторов  и отстоят друг от друга на межплоскостное расстояние . С другой стороны, из формул (1.1), (1.6), (2.6) следует, что

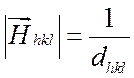                                           .                                          (2.9)

Итак, вектор обратной решетки кристалла  направлен перпендикулярно к кристаллографической плоскости с индексами , а его модуль равен обратной величине межплоскостного расстояния .

Так как пространственное расположение атомов в каждой элементарной ячейке одинаково, то суммирование в формуле (1.13), так же как и интегрирование в выражениях (1.8), (1.9), проводят по объему одной элементарной ячейки. Если при этом учесть, что для кристаллов , то выражение (1.13) перепишется следующим образом:

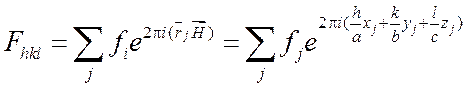                             .         (2.10)

Величину  называют структурной амплитудой отражения .

Сильные «отражения» от кристалла, то есть большая величина , получаются тогда, когда кристаллографическая плоскость , к которой перпендикулярен вектор , густо «заселена» атомами. Это утверждение справедливо и для некристаллических объектов при отсутствии кристаллографических плоскостей. В таких объектах можно выделить плотно «заселенные» слои или ряды атомов. Тогда по аналогии с кристаллами функция  имеет наибольшие значения, когда вектор  перпендикулярен к этим рядам или слоям.

Как было отмечено выше, только узлы обратной решетки, которые попадают на сферу Эвальда, соответствуют дифракции (см. рис. 2.4). В случае обычных низкомолекулярных кристаллов узлы обратной решетки располагаются редко, т.к. их периоды  велики из-за малости периодов решетки . Чтобы увеличить число пересечений со сферой отражения, пользуются различными приемами, например уменьшают длину волны рентгеновского излучения, различным образом перемещают кристалл (методы вращающегося или колеблющегося кристалла). В случае же монокристаллов белков периоды  больше. Следовательно, становятся более вероятными из-за малости периодов  попадания узлов обратной решетки на сферу Эвальда. Поэтому даже неподвижный монокристалл белка дает богатую «рефлексами» («отражениями») дифракционную картину (рентгенограмму) (рис. 2.6).

Рис. 2.6. Рентгенограмма миоглобина кашалота

Из сказанного ранее следует, что рентгенограмма в принципе является изображением обратной решетки кристалла. Рассеянные лучи направлены вдоль образующих конусов с вершинами в центре сферы отражений и при регистрации на плоскую фотопленку пересекаются с ней по кривым второго порядка. Поэтому существуют различные методы получения неискаженных изображений обратной решетки, суть которых сводится к одновременному движению кристалла и пленки, плоскость которой остается параллельной выбранной плоскости обратной решетки.

Из рентгенограммы можно получить информацию о межплоскостных расстояниях, размерах ячеек, числе атомов в ячейках. Но основные сведения о распределении электронной плотности в кристаллах получают путем анализа интенсивностей рассеянных рентгеновских пучков, которые определяются также из рентгенограмм. Интенсивность рефлекса, который дает узел обратной решетки, определяемый вектором , связанным с соответствующим углом  по формуле (1.6), дается выражением

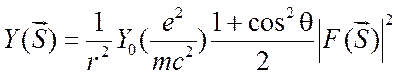                            ,                    (2.11)