Обработка биомедицинских сигналов: Учебное пособие, страница 4

Вычисление спектральных коэффициентов A_j в этом случае производится по формуле:

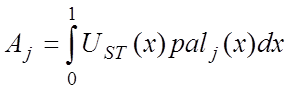.                                     (12)

Рис. 7. Функции Уолша (упорядочение по Уолшу)

3. ДИСКРЕТИЗАЦИЯ И КВАНТОВАНИЕ БИОМЕДИЦИНСКИХ СИГНАЛОВ

3.1.  Дискретизация

Как отмечалось, при дискретизации непрерывный сигнал представляется дискретными отсчетами, взятыми через определенный промежуток времени, называемый шагом дискретизации. Обозначим этот промежуток времени Δt. Каковы же критерии выбора  шага дискретизации Δt?

Все реальные сигналы имеют конечную протяженность во времени. Известно, что функция конечной длительности обладает теоретически бесконечным спектром [1]. В то же время у всех реальных непрерывных сигналов основная часть спектра сосредоточена в конечной полосе частот, называемой практической шириной спектра. Начиная с некоторой частоты, составляющие высокочастотной части спектра сигналов оказываются ниже уровня помех, имеющихся в линиях передачи и преобразования сигналов, и не воспринимаются получателем. Поэтому можно ввести идеализацию, заключающуюся в том, что все реальные непрерывные сигналы рассматриваются как функции с ограниченным спектром. Это функции, спектр которых не содержит частот выше некоторой граничной частоты Fc.

Различные биомедицинские сигналы имеют и различные граничные частоты Fc. Так, сигналы температуры тела имеют граничную частоту 0.1 Гц, частота дыхания – 2 Гц, реограмма – 50 Гц, электрокардиограмма и электроэнцефалограмма – 100 Гц, фонокардиограмма – 1000 Гц  [2]. В этом случае величина шага дискретизации ставится в зависимость от наивысшей частоты  в спектре сигнала. Правило выбора предельного максимального шага дискретизации для сигналов, моделью которых является функция  с ограниченным спектром, сформулировано и доказано академиком В. А. Котельниковым в 1933 году в виде теоремы.

Теорема В. А. Котельникова

Сигнал, описываемый функцией с ограниченным спектром, полностью определяется своими значениями, отсчитанными через интервалы времени

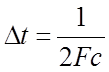                                                       ,                                                            (13)

где Fc – ширина спектра сигнала.

Представление непрерывного сигнала его дискретными отсчетами при этом имеет вид

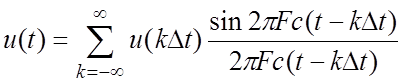                             .                               (14)

Выражение (14) называют рядом В. А. Котельникова. Из сравнения (14) и (1) следует, что ряд В. А. Котельникова является частным случаем обобщенного ряда Фурье.

Поскольку реальные сигналы имеют конечную длительность во времени, то такие сигналы в соответствии с теоремой  В. А. Котельникова можно представить конечным числом отсчетов

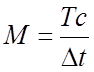                                                       ,                                                              (15)

где Тс – время существования непрерывного сигнала.

Для реальных сигналов, имеющих ограниченное время существования, ряд (14) можно записать в виде

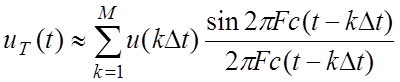                             .                                       (16)

Приближенность выражения (16) проявляется в том, что при конечном числе членов ряда их сумма точно совпадает с мгновенными значениями сигнала u(t) не на всем интервале Тс, а только в точках отсчетов. В промежутках между отсчетами сигнал u(t) заменяется суммой базисных функций с соответствующими масштабными коэффициентами u(kΔt), поэтому ограничение числа слагаемых приводит к отличию восстановленного сигнала от исходного, то есть к появлению погрешности, связанной с дискретизацией. Уменьшить эту погрешность можно только за счет увеличения числа членов ряда. Как следует из выражения (15), при конечной длительности Тс это возможно только при уменьшении шага дискретизации. Назовем этот новый шаг дискретизации, который обеспечивает заданную погрешность представления непрерывного сигнала дискретными отсчетами, периодом дискретизации и обозначим Тд, а дискретные отсчеты –  u(kT_Д). 

Восстановление непрерывной функции времени по ее дискретным отсчетам может быть выполнено двумя способами: фильтрационным и интерполяционным. Наибольшее применение в настоящее время имеет интерполяция нулевого, первого и второго порядков (ступенчатая, линейная и параболическая) на основе интерполяционного многочлена Лагранжа соответствующего порядка.

Для каждого из перечисленных видов интерполяции период дискретизации Тд связан с шагом дискретизации, определяемым теоремой В. А. Котельникова из выражения (13), соотношениями [9]: при ступенчатой интерполяции

                                          ;                                                       (17)

при линейной интерполяции

                                          ;                                         (18)

при параболической интерполяции

                                          ,                                                               (19)

где δ₀ – допустимая относительная погрешность равномерного приближения, определяемая выражением

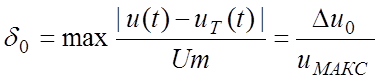                                          ,                                  (20)

где u(t) – исходный непрерывный сигнал,

u_т(t) – сигнал, восстановленный по отсчетам с помощью соответствующего вида интерполяции,

Um=u_макс – полная шкала изменения мгновенных значений исходного       сигнала.

3.2. Квантование

Квантование сигналов, как отмечалось выше, заключается в замене текущего значения непрерывного сигнала u(t) или u(kT_Д) одним из конечного числа N уровней квантования. Обозначим номера уровней квантования как 0, 1, 2, … , N-1.

Наиболее часто применяют равномерное квантование, при котором расстояние ΔU между двумя соседними уровнями, называемое шагом квантования, одинаковое  для всего диапазона изменения непрерывного сигнала.

Шкала U значений сигнала в произвольный момент времени t_i, который при дискретизации сигналов совпадает с моментами взятия дискретных отсчетов kТ_Д, может быть разбита на отдельные уровни квантования различными способами (рис. 8).

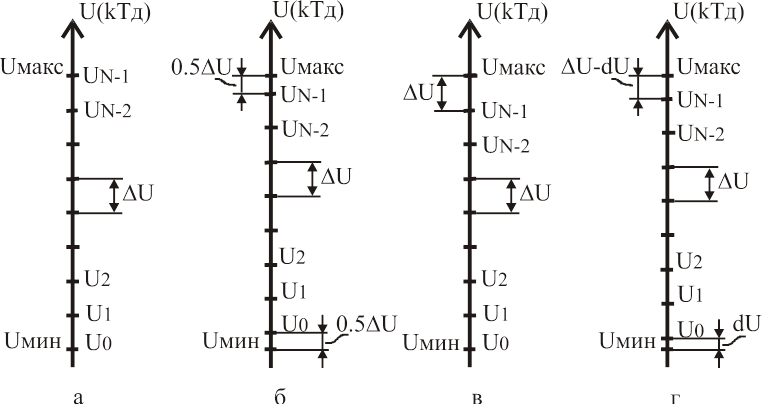
Рис. 8.  Способы разбиения шкалы сигнала на отдельные уровни