Обработка биомедицинских сигналов: Учебное пособие, страница 3

где d_kj – символ Кронекера, равный 1 при k=j и 0 при k¹j,

* - символ комплексной сопряженности. 

Постоянная E_k физически соответствует энергии сигнала j_k(t). Величину  называют нормой базисной функции j_k(t).

Для действительных функций j_k(t), k=0, 1, 2,…, условие ортогональности имеет вид

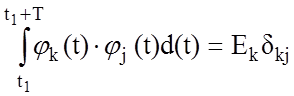                                         .                                        (4)

Система ортогональных функций является частным случаем системы линейно независимых функций.

На практике часто пользуются ортонормированной системой функций {y_k(t)}, которая образуется из системы ортогональных функций {j_k(t)} нормировкой каждой функции по ее норме, т. е. делением на норму

                                               .                                                  (5)

Коэффициенты ряда (1) находятся следующим образом. Умножим обе части равенства (1) на j_j^*(t) и проинтегрируем на интервале (t₁, t₁+T):

                    .

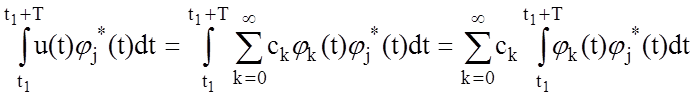С учетом выражения (3) получим

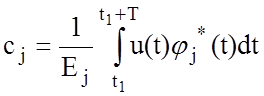                                               ,   j=0, 1, 2, …             (6)

При использовании ортонормированной системы

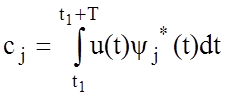                                     ,   j=0, 1, 2, …                                          (7)

Представление сигнала в виде (1) называют обобщенным спектром   Фурье. Коэффициенты с_j, определяемые (6) или (7), называют обобщенными коэффициентами Фурье.Совокупность коэффициентов с_j и порядковых номеров функций называют обобщенным спектром сигнала.

2.2. Системы базисных функций, применяемые при обработке         биомедицинских сигналов

Цель обработки биомедицинских сигналов – выявление информативных параметров, характеризующих функциональное состояние контролируемых систем организма, запоминание этих параметров и представление их в виде, удобном для восприятия, анализа и принятия решения потребителем  (врачом-диагностом, лечащим врачом).

В связи с этим к ортогональным базисным функциям, применяемым при обработке биомедицинских сигналов, можно предъявить дополнительно следующие требования:

·  ряд (1) должен сходиться как можно быстрее при сохранении точности оценок параметров биомедицинского сигнала;

·  разные информативные параметры сигнала должны описываться  минимальными наборами спектральных коэффициентов, в пределе один параметр – один спектральный коэффициент (требование локализации).

Выполнение этих требований обеспечит уменьшение объема памяти средств обработки, количества вычислительных операций, необходимых для обработки сигнала.

Наиболее часто в настоящее время используются система тригонометрических функций и система комплексных экспоненциальных функций.

Система тригонометрических функций

  {φ_k(t)}={φ₀(t)≡1, φ_k^C(t)=сos(kΩ₁t), φ_k^S(t)=sin(kΩ₁t)}, k=1, 2, 3, …, 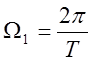,       (8)

где с и s – индексы, обозначающие четность и нечетность функции соответственно.

Система (8) является полной и ортогональной на любом интервале длиной Т.

Функция  имеет норму . Для остальных функций норма равна .

Система комплексных экспоненциальных функций

 {φ_k(t)}={exp(jkΩ₁t}, k=…-2, -1, 0, 1, 2, …, 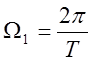.                                   (9)

Система (9) является полной и ортогональной на любом интервале длиной Т. Все функции имеют норму .

Системы (8) и (9)  используются для разложения на элементарные составляющие сигналов любой формы, имеющих период повторения Т, а также сигналов, заданных только на интервале длиной Т.

В биомедицинской практике системы (8) и (9) применяются для анализа вариабельности сердечного ритма [4, 5], анализf низкоамплитудных потенциалов в биомедицинских сигналах, в частности поздних потенциалов желудочков [6,  7].

В ряде случаев представление биомедицинского сигнала суммой гармонических составляющих в соответствии с (8) и (9) не позволяет явно выразить  информативный параметр ограниченным набором спектральных коэффициентов. Например, для информативных параметров ST-сегмента электрокардиосигнала, смещения и наклона относительно изолинии, выпуклости,  только смещение представляется одним спектральным коэффициентом С₀ при равенстве нулю всех остальных спектральных коэффициентов (рис. 5,а). Остальные же параметры характеризуются множеством спектральных коэффициентов, причем разным значениям этих параметров соответствует свой набор спектральных коэффициентов (рис. 5,б,в). Это обстоятельство делает  практически невозможным оценивать информативные параметры ST-сегмента спектральными коэффициентами упомянутых выше базисов (8) и (9).

Исследования показывают, что применительно к анализу параметров ST-сегмента предпочтительнее использовать базисы на основе полиномов Лежандра и функций Уолша.

а
б
в

Рис. 5. Гармонические спектры сигналов, моделирующих

различные типы формы ST-сегмента

Полиномы Лежандра

Полиномы Лежандра L_n(x) – многочлены, ортогональные на отрезке [-1,1] с единичной весовой функцией h(x)=1. Они определяются выражением [8]:

и удовлетворяют рекуррентному соотношению:

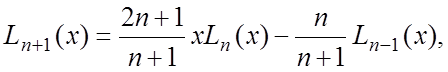                               (10)

при этом L₀(x)=1,L₁(x)=x.

Полиномы Лежандра ортогональны, а именно:

 .

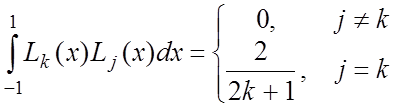На рис. 6 представлен вид первых четырех полиномов Лежандра.

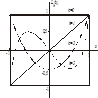
Рис. 6. Полиномы Лежандра

Вычисление спектральных коэффициентов cL_j производится по формуле:

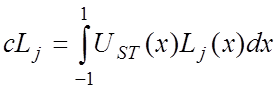                .                                         (11)

Система функций Уолша

Функции Уолша – кусочно-непрерывные ступенчатые функции, ортонормированные на отрезке [0,1] и принимающие на указанной области определения два дискретных значения:  +1 и –1 [3] (рис. 7).

Упорядоченность функций в системе производится по числу пересечений ими нулевого уровня. Существуют три подхода к порядковой нумерации функций Уолша (по Уолшу, Пэли и Адамару). Ниже будут более подробно описаны процесс формирования функций Уолша и процесс их упорядочения. Здесь же отметим, что при обработке кардиосигнала для выявления информативных параметров ST-сегмента предпочтительнее использовать функции Уолша, упорядоченные по Пэли.