Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 4

     Принцип ординарности потока. Поток считается ординарным (простым), если за интервал времени t может наступить не более одного события. Для доказательства ординарности потока, записанного пуассоновского распределением, выполним следующие преобразования. Допустим, за интервал времени t в потоке не наступило ни одного события, то есть можно записать k=0, тогда

                                                 .

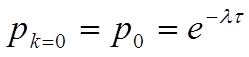Вероятность того, что за время t наступит одно событие:

                                                .   

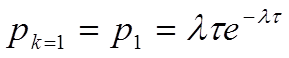   Если сложить вероятности  и , получим

                           .    

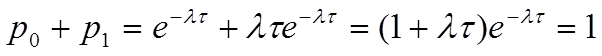     Из этого следует, что за интервал времени t в простейшем потоке может наступить не более одного события.

     Отсутствие последействия в потоке. Это значит, что прошлое событие не влияет на вероятность появления последующих событий. Это условие вытекает из

определения пуассоновского распределения. Отсутствие последействия позволяет вместо моментов наступления события t_i вычислять интервалы времени между событиями t. В этом случае момент наступления каждого последующего события будет определяться суммой момента наступления предыдущего события t_i-1 и интервала времени между этими событиями:

                                                  .   

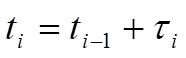Следовательно, для моделирования потока, в котором необходимо определить t_i,

достаточно знать закон распределения t_i. Зная закон распределения t_I, можно легко имитировать события потока (моменты наступления). Для этого достаточно обратиться к датчику случайных чисел с установленным законом распределения. Датчик  выдает случайные числа, равные t_i.

     Докажем, что в простейшем потоке t_i подчиняется показательному закону распределения. Функцию распределения для t можно записать в виде:

                                   , где t одно из значений t.

Тогда вероятность того, что случайная величина t не примет ни одного из значений меньше или равно t, запишется в виде:   

                                  .

Из пуассоновского распределения следует, что

                                 .

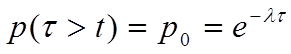В этом случае

                                 .

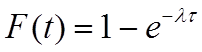Это запись показательного закона распределения, для которого плотность распределения записывается в ви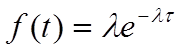де:

                , где - интенсивность, m(t) – математическое ожидание.

2. 1. 2. Моделирование обслуживающих аппаратов

     Математической моделью обслуживающего аппарата является запись, с помощью которой можно определить состояние системы (обслуживающих аппаратов) в любой момент времени. Если входные потоки простейшие, то для математического описания обслуживающих аппаратов можно использовать теорию марковских процессов. Под марковским процессом понимается последовательность состояний системы. Вероятность каждого из состояний системы не зависит от того, из какого состояния система перешла в искомое состояние, а определяется вероятностью настоящего состояния и вероятностью перехода. В марковском процессе фигурируют два независимых события:

1)  система находится в настоящий момент в конкретном состоянии;

2)  под воздействием управления система перейдёт (или не перейдет) в другое  состояние.

     Допустим, под воздействием входного потока и потока обслуживания система может переходить в состояния S₀ (начальное состояние), S₁, S₂, …, S_n (конечное состояние). Для того чтобы описать эти состояния, необходимо найти вероятность перехода системы из S_i в S_j за время t  (p_ij(t)). Если принять, что в момент времени t₀ (в прошлом) система находилась в состоянии S₀, а к моменту времени t (настоящее время) система находится в состоянии S_i, и в момент времени (будущее) система будет находиться в состоянии S_j, то в соответствии с формулой Маркова (модель марковского процесса) вероятность перехода системы из i-го состояния в j-ое;

             .

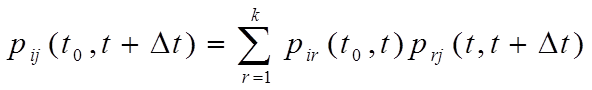    В формуле принято, что в момент времени t₀ система находилась в состоянии S_i,в момент времени t система находится в состоянии S_r,а в момент времени  система будет находиться в состоянии S_j.

p_ir(t₀, t) определяет вероятность перехода системы к моменту времени t из состояния S_i в промежуточное S_r. p_rj (t, t+Dt) определяет вероятность перехода системы к моменту времени t+Dt из промежуточного состояния S_r в конечное искомое состояние.

     Как правило, в исходном описании системы дается значение вероятности начального состояния системы и вероятности одношагового перехода системы из одного состояния в другое.

     Для описания динамики поведения системы обслуживания (обслуживающего аппарата) Колмогоровым на основе уравнения Маркова была предложена система дифференциальных уравнений вероятностей состояния системы. Допустим, что система находится в состоянии S_i. Известны интенсивности перехода из состояния S_i в возможные состояния S_j (интенсивности обозначаются l_ij(t)). Граф такой системы имеет вид рис. 4.

lii

                                               

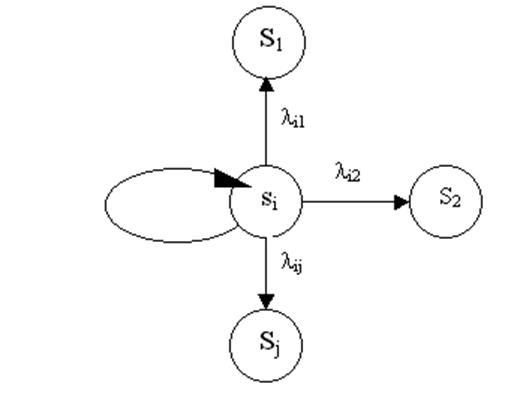
Рис. 4

     Пользуясь уравнением Маркова, Колмогоров составил систему дифференциальных уравнений вида:

                                         .

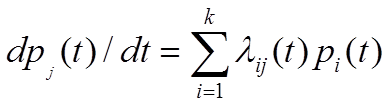     Как правило, в момент времени t=0 известны p_i(0) и l_ij(0).

2. 1. 3. Методика составления дифференциальных уравнений

Колмогорова

 Уравнения Колмогорова составляются в следующей последовательности:

1.Задаются возможные состояния системы (допустим, s₁, s₂, s₃, s₄).

2.Определяются интенсивности переходов из состояния в состояние l_ij.

3.Строится граф системы, вершинами которого являются состояния, дугами - интенсивности переходов. В рассматриваемом случае граф имеет вид рис. 5.

                                                                l₄₁

                                                                l₁₄

                                                  l₄₃                 l₄₂

                                      l₃₄                   l₂₄                     l₂₁

                                                                l₃₂

Рис. 5