GENE 10000,,,1
TERM 1
STAR 1
END
По окончанию моделирования из стандартного отчёта
находим: 
=0,46; так как число поступивших
требований Nпост.=108,
а обслуженных - Nобсл.=66,
то R = 66/108.
2. 4. Статистическая обработка результатов эксперимента на имитационной модели
Часто целью моделирования является определение функциональной зависимости между параметрами объекта. Как правило, такая зависимость случайная, поэтому полученные результаты подвергаются статистической обработке.
Допустим, в результате эксперимента на модели необходимо найти зависимость параметра y от параметра x, то есть y = f(x).
Обработка ведётся в следующей последовательности:
1. Определяются статистические средние (оценки математических ожиданий) параметров y и x по формулам:
;
,
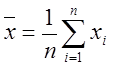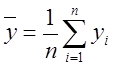где xi и yi – это фактические результаты, полученные в ходе эксперимента.
2. Устанавливается функциональная зависимость между параметрами x и y.
Для дальнейшего упрощения поиска этой зависимости она представляется в линейном виде: y = a0 + a1x. Если искомая зависимость нелинейная, её необходимо свести к линейному виду путём замены переменных.
например: y = a0 + a1/x, x’ = 1/x => y = a0 + a1x’;
y = a0*e a1x, y = ey1 => y1 = ln a0 + a1x.
3. В полученной линейной зависимости определяется, на сколько параметры x и y линейно зависимы друг от друга. Оценку линейной зависимости производят с помощью коэффициента корреляции R
R =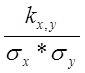 
,
где kx, y – момент корреляции между
x и y;
- средние квадратичные отклонения по x и y.
Коэффициент R в линейной зависимости изменяется от -1 до +1. Если R – отрицательный, зависимость – обратная; если R = 0, зависимость отсутствует.
Коэффициент R на основе статистических данных определяется по формуле
.
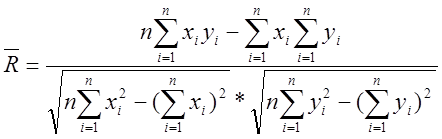Если R по абсолютному
значению окажется меньше 0,3, то зависимость между x и y –
слабая (
). Если окажется, что 
зависимость – сильная. В промежутке 
- средняя зависимость.
Допустим, зависимость между x и y оказалась средняя и выше. В этом случае переходят к пункту 4.
4. Определяется количественное значение коэффициентов а0 и а1 по методу наименьших квадратов. Для этого определяется сумма квадратов отклонений yi экспериментального от теоретических значений (yi = a0 + a1xi) по формуле
.
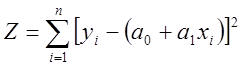Полученное Z является функцией двух коэффициентов: а0 и а1. Их необходимо подобрать таким образом, чтобы теоретическое значение yi мало отличалось от экспериментального значения yi. А это значит, найти такие значения а0, а1, при которых Z принимала бы минимальное значение. Минимум функции Z можно найти из системы уравнений с частными производными приравненными к нулю. В данном случае имеем два уравнения с частными производными:
;
.
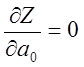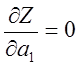Решив указанную систему, найдём искомые коэффициенты а0 и а1. Поиск осуществляется следующим образом. Дифференциальные уравнения записываются на основе статистических данных в виде:
.
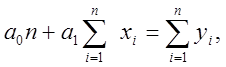
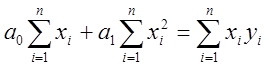Решая указанную систему, определим коэффициенты по формулам:
;
.
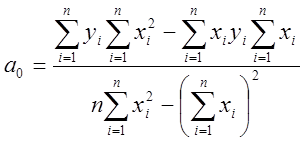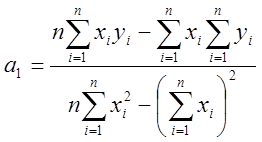5. После того, как значения коэффициентов определены,
устанавливается их значимость в функциональной зависимости, т.е. определяется,
насколько их значение влияет на зависимость одного параметра от другого.
Значимость коэффициентов находится путём сравнения случайных величин tф с tтеор., где
t – случайная величина, подчиняющаяся t-распределению
и задана таблично для выбранной степени свободы V и уровня
доверия 
(доверительная вероятность). В
рассматриваемом случае выбираем V=2. Затем tф для каждого из коэффициентов определяется по формуле
taj =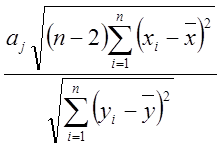 
, j – индекс коэффициента (j = 0,1).
Если окажется, что tф
tтеор., то соответствующий коэффициент незначителен и им
можно пренебречь.
2. 5. Проверка адекватности модели
Модель считается адекватной, если полученные на ней результаты близки к результатам, полученным на объекте при тех же условиях. Адекватность модели обычно проверяется по каждому из параметров р в отдельности, т.е. собирают статистические данные по одному из параметров на объекте и на модели. Остальные параметры принимают неизменными.
Адекватность проверяется или по соответствию средних значений случайной величины (параметра), или по соответствию дисперсий случайной величины (параметра).
1. Проверка адекватности модели по средним значениям параметра
Для этого на объекте и на модели проводится N –
независимых испытаний. По результатам испытаний находят средние значения
откликов (результатов) по параметру р на объекте - 
и
на модели - 
; по формулам:
; 
.
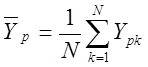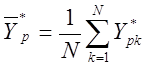Определяют оценку дисперсии на объекте - 
и на модели - 
по формулам: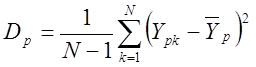 
; 
.
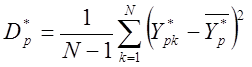Вычисляют величину отклонения средних откликов на
модели и объекте: 
, определяют дисперсию
полученной ошибки 
по формуле: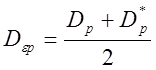 
и tтеор. для выбранного и
V = 2(N-1) и tф по
формуле: tф =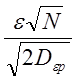 
. Если окажется, что tф
tтеор. –
модель по параметру р адекватна. Если условие не выполняется, модель по данному
параметру не адекватна.
2. Проверка адекватности по дисперсиям
Для этого по каждому параметру р вычисляется дисперсия
по выше изложенной формуле на объекте - и
на модели по формуле
.
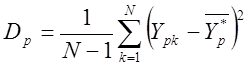Далее вычисляется случайная величина F, которая подчиняется распределению Фишера, она задана таблично и несёт информацию о соотношении дисперсии.
Из табличных данных при выбранном и степени свободы V1=V2=N выбирается
Fтеор.
Затем вычисляется Fфакт.=
. Если Fф Fт, модель по дисперсии по параметру р адекватна. Если
условие не выполняется, модель не адекватна и переходят к её калибровке.
2. 6. Калибровка модели
Калибровкой называется изменение структуры и состава модели таким образом, чтобы отредактированная модель бала адекватна по каждому из параметров р, установленных в модели.
Калибровка проводится в 3 этапа. На каждом из этапов используются специальные средства калибровки модели и оценки адекватности по каждому из параметров.
1.
Калибровку модели проводят путем
сравнения распределения вероятности результатов, полученных на объекте -
и на модели - 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.