Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 8

Переменными транспортной задачи являются , , , - объемы перевозок от i-го поставщика j- му потребителю. Эти переменные можно записать в виде матрицы перевозок

.

Так как - это затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны 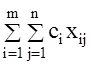, требуется обеспечить минимум суммарных затрат. Система ограничений задачи состоит из двух групп уравнений. Первые m уравнений описывают тот факт, что запасы всех поставщиков вывозятся полностью. Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех потребителей.

Учитывая условие неотрицательности объемов перевозок, математическую модель задачи можно записать так:

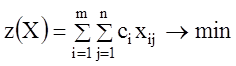                    (1.47)

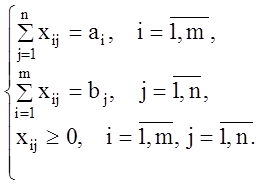                            (1.48)

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

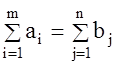.                               (1.49)

Определение 1.21. Условие (5.49) называется условием баланса. Модель в этом случае называется закрытой.

Определение 1.22. Если равенство (5.49) не выполняется, то модель называется открытой.

Теорема 1.11. Для того чтобы транспортная задача имела решение, необходимо и достаточно, чтобы выполнялось условие баланса (1.49).

Теорема 5.12. Ранг системы векторов условий транспортной задачи равен .

Из теоремы 1.12 следует, что опорный план не может иметь более  координат, отличных от нуля. Следовательно, невырожденный опорный план транспортной задачи имеет  положительных координат, а вырожденный опорный план имеет меньше чем  положительных координат.

Любой допустимый план можно записать в виде таблицы.

Определение 1.23. Клетки таблицы, в которых находятся отличные от нуля перевозки, называются занятыми, остальные - свободными.

Для проверки линейной независимости векторов условий, соответствующих положительным координатам допустимого плана, а также для построения нового опорного плана используется понятие цикла.

Определение 1.24. Циклом называется последовательность клеток таблицы транспортной задачи , , , …, , в которой две соседние клетки находятся либо в одной строке, либо в одном столбце, причем первая и последняя клетки так же находятся в одной строке или столбце.

Построение циклов начинают с какой-либо незанятой клетки и переходят по столбцу (строке) к другой занятой клетке, в которой делают поворот под прямым углом и двигаются к следующей незанятой клетке и т.д., пытаясь вернуться к первоначальной клетке.

Теорема 1.13. Для того чтобы система векторов условий транспортной задачи была линейно зависимой, необходимо и достаточно, чтобы из соответствующих занятых клеток таблицы можно было построить цикл.

Следствие. Допустимый план транспортной задачи является опорным тогда и только тогда, когда из занятых клеток таблицы нельзя образовать ни одного цикла.

Основные этапы решения сбалансированной транспортной задачи следующие.

1.  Построение математической модели исходной задачи.

2.  Применение алгоритма метода решения транспортной задачи:

1)  составление задачи двойственной исходной;

2)  определение первоначального плана перевозок;

3)  проверка полученного плана на оптимальность;

4)  переход к новому плану перевозок;

5)  проверка вновь полученного плана на оптимальность.

Затем этапы 4 и 5 повторяются до тех пор, пока не будет получен оптимальный план или выяснится, что задача не имеет решения.

Первоначальный опорный план транспортной задачи как задачи ЛП можно построить ранее рассмотренными методами, однако это связано с большими вычислениями. Существуют несколько простых методов построения первоначального опорного плана транспортной задачи, которые рассмотрим на примерах.

Пример 5.8. Найти начальный опорный план транспортной задачи, условия которой заданы в виде табл. 1.6.

     Таблица 1.6

		100	80	90	80
	80	2	1	3	4
	120	4	3	1	7
	150	5	8	9	15

Решение.

Метод «северо-западного угла»

Не учитывая стоимость перевозок, начинаем удовлетворение потребностей первого потребителя за счет запасов первого поставщика. Для этого сравниваем ед. с ед., , тогда 80 записываем в клетку (1,1). Запасы 1-го поставщика полностью израсходованы, поэтому в остальных клетках 1-й строки ставим прочерки. Потребности 1-го потребителя полностью не удовлетворены на 100-80=20 ед. Сравниваем этот остаток с запасами 2-го поставщика и, поскольку , в клетку (2,1) записываем 20. Теперь потребности 1-го потребителя удовлетворены, поэтому в 1-м столбце в остальных клетках ставим прочерк. У 2-го поставщика осталось ед. груза, удовлетворяем потребности 2-го потребителя. Для этого сравниваем остаток у 2-го поставщика с потребностями 2-го потребителя. Имеем

,

поэтому в клетку (2,2) записываем 80, потребности 2-го потребителя полностью удовлетворены, поэтому в остальных клетках второго столбца ставим прочерк. У 2-го поставщика осталось ед., их используем для удовлетворения  потребностей  3-го  потребителя и т.д.  В итоге получаем следующую табл. 1.7.

Таблица 1.7

		100	80	90	80
	80	80	¾	¾	¾
	120	20	80	20	¾
	150	¾	¾	70	80

Метод минимальной стоимости

Составим с помощью этого метода опорный план уже рассмотренной задачи.